Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chị ơi giúp e cái này tìm 3 giá trị của x sao cho 0,6<x<0,61
Gọi I là tâm đường tròn nội tiếp tam giác ABC
\(\Rightarrow a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\)
Ta có:
\(A=\left|a\overrightarrow{MA}+b\overrightarrow{MB}+c\overrightarrow{MC}\right|=\left|\left(a+b+c\right)\overrightarrow{MI}+a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right|\)
\(=\left|\left(a+b+c\right)\overrightarrow{MI}\right|=\left(a+b+c\right).MI\)
\(Amin\Leftrightarrow MImin\)
\(\Leftrightarrow\) M trùng I

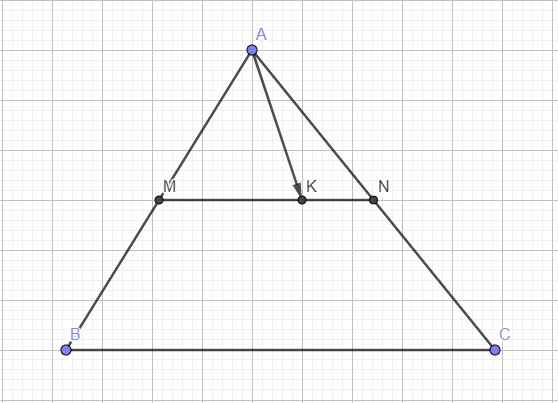
MN là đường trung bình của tam giác ABC
\(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Từ giả thiết:
\(\overrightarrow{KM}=-2\overrightarrow{KN}=-2\left(\overrightarrow{KM}+\overrightarrow{MN}\right)\)
\(\Rightarrow3\overrightarrow{KM}=2\overrightarrow{NM}\Rightarrow\overrightarrow{KM}=\dfrac{2}{3}\overrightarrow{NM}\)
\(\Rightarrow\overrightarrow{MK}=\dfrac{2}{3}\overrightarrow{MN}=\dfrac{2}{3}\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
Do đó:
\(\overrightarrow{AK}=\overrightarrow{AM}+\overrightarrow{MK}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

a) Có \(\overrightarrow{BC}^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
Suy ra: \(\overrightarrow{AC}.\overrightarrow{AB}=\dfrac{\overrightarrow{AC^2}+\overrightarrow{AB}^2-\overrightarrow{BC}^2}{2}=\dfrac{8^2+6^2-11^2}{2}=-\dfrac{21}{2}\).
Do \(\overrightarrow{AC}.\overrightarrow{AB}< 0\) nên \(cos\widehat{BAC}< 0\) suy ra góc A là góc tù.
b) Từ câu a suy ra: \(cos\widehat{BAC}=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=-\dfrac{21}{2.6.8}=-\dfrac{7}{32}\).
Do N là trung điểm của AC nên \(AN=AC:2=8:2=4cm\).
\(\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cos\left(\overrightarrow{AM},\overrightarrow{AN}\right)\)
\(=2.4.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=2.4.\dfrac{-7}{32}=-\dfrac{7}{4}\).

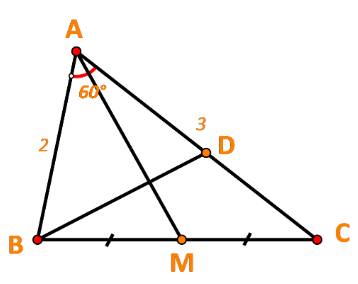
a) \(\overrightarrow {AB} .\overrightarrow {AC} = 2.3.\cos \widehat {BAC} = 6.\cos {60^o} = 3\)
b)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)(do M là trung điểm của BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
+) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} \)
c) Ta có:
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {BD} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right)\left( {\frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} } \right)\\ = \frac{7}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{7}{{24}}{\overrightarrow {AC} ^2} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \\ = - \frac{1}{2}A{B^2} + \frac{7}{{24}}A{C^2} - \frac{5}{{24}}\overrightarrow {AB} .\overrightarrow {AC} \\ = - \frac{1}{2}{.2^2} + \frac{7}{{24}}{.3^2} - \frac{5}{{24}}.3\\ = 0\end{array}\)
\( \Rightarrow AM \bot BD\)

Lời giải:
\(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BO}+\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}=2\overrightarrow{BO}+(\overrightarrow{OA}+\overrightarrow{OC})\)
\(=2\overrightarrow{BO}\) (do $\overrightarrow{OA}, \overrightarrow{OC}$ là 2 vecto đối)
Và:
\(\overrightarrow{BE}+\overrightarrow{BF}=\overrightarrow{BO}+\overrightarrow{OE}+\overrightarrow{BO}+\overrightarrow{OF}=2\overrightarrow{BO}+(\overrightarrow{OE}+\overrightarrow{OF})\)
\(=2\overrightarrow{BO}\) (do $\overrightarrow{OE}, \overrightarrow{OF}$ là 2 vecto đối)
Vậy \(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{BF}\)

1.
Gọi G là trọng tâm tam giác
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{OG}=\overrightarrow{0}\)
\(\Leftrightarrow O\equiv G\)
\(\Rightarrow O\) là trọng tâm tam giác ABC
\(\Rightarrow\Delta ABC\) đều
Gọi độ dài các cạnh tam giác là a
\(\overrightarrow{BN}.\overrightarrow{AM}=\dfrac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=-\dfrac{1}{4}a^2-\dfrac{1}{8}a^2-\dfrac{1}{8}a^2+\dfrac{1}{2}a^2=0\)
Mặt khác \(\overrightarrow{BN}.\overrightarrow{AM}=BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)\)
\(\Rightarrow BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow\left(\overrightarrow{AM};\overrightarrow{BN}\right)=90^o\)
\(BD=\dfrac{AB}{cos45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{BQ}.\overrightarrow{BP}=\dfrac{1}{4}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{4}BA.BC.cos90^o+\dfrac{1}{4}BA.BD.cos45^o+\dfrac{1}{4}BD.BC.cos45^o+\dfrac{1}{4}BD^2\)
\(=\dfrac{1}{4}a^2+\dfrac{1}{4}a^2+\dfrac{1}{2}a^2=a^2\)


Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)
\( \Rightarrow \overrightarrow {NC} = - \overrightarrow {NB} \)
Do đó: \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} = \overrightarrow {NC} + \overrightarrow {CM} \)(tính chất giáo hoán)
\( \Rightarrow \overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {NM} \Leftrightarrow \;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)
Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)
Vậy \(\;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \frac{a}{2}.\)