Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

KHÔNG THẤY HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP NHA
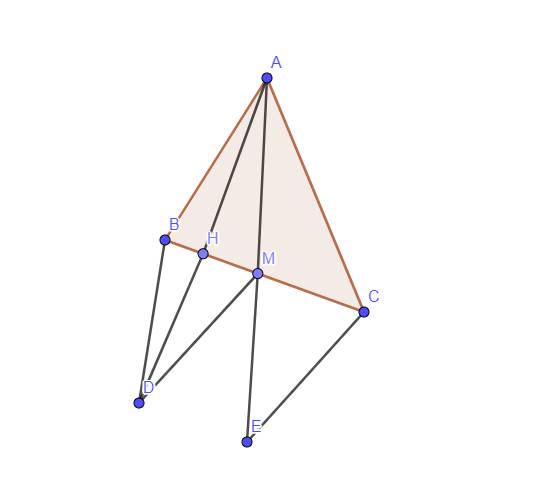
A) VÌ \(BH\perp AD\Rightarrow\widehat{BHA}=90^o\)
\(CI\perp AD\Rightarrow\widehat{CID}=90^o\)
\(\Rightarrow\widehat{BHA}=\widehat{CID}=90^o\)hay \(\widehat{BHI}=\widehat{CIH}=90^o\)
HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
=> BH // CI (ĐPCM)
B)
XÉT \(\Delta ABC\)VUÔNG TẠI A
\(\Rightarrow\widehat{A}=90^o\)hay \(\widehat{BAH}+\widehat{HAC}=90^o\left(1\right)\)
XÉT \(\Delta AHB\)VUÔNG TẠI H
\(\Rightarrow\widehat{H}=90^o\)hay \(\widehat{BAH}+\widehat{ABH}=180^o-90^o=90^o\left(2\right)\)
từ (1) và (2) \(\Rightarrow\widehat{HAC}=\widehat{ABH}\)
XÉT \(\Delta ABH\)VÀ\(\Delta CAI\)CÓ
\(\widehat{H}=\widehat{I}=90^o\)
AB = AC (gt)
\(\widehat{ABH}=\widehat{IAC}\)(CMT)
=>\(\Delta ABH\)=\(\Delta CAI\)(C-G-C)
=> BH = AI ( HAI CẠNH TƯƠNG ỨNG )

Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath

Lời giải:
a.
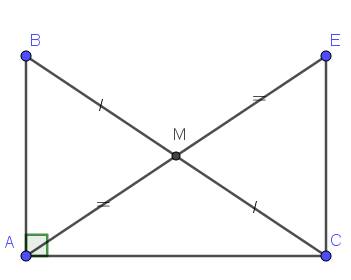
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

C/m : ^KEC=^BCA
Xet : 2 tg :tgKEC=tgBCA
Có : CE cạnh chung
^MCE = ^CEK (slt) (vi : CE//AB ( tgAMB=tgEMC))
^ECK=^MEC (slt) (vi : CE//AB(tgAMB=tgEMC))
=> tgKEC=tgBCA
=>^KEC=^BCA
*chú ý : "^" là góc ; tg là viết tắt của tam giác .
được rồi chứ bạn

a: Xét ΔAMB và ΔEMC co
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xet ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔAMD có
MH vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại M

#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.