a) Trong tam giác ABC: \(\widehat C = 180^\circ  - \widehat A - \widehat B = 180^\circ  - 42^\circ  - 37^\circ  = 101^\circ \).

b) Trong tam giác ABC: \(\widehat B < \widehat A < \widehat C\)nên \(AC < BC < AB\). (Vì AC đối diện với góc B; BC đối diện với góc A; AB đối diện với góc C). 

a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm

Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC

Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :

\( \Rightarrow \widehat A > \widehat B > \widehat C\)

b)

Vì \(\widehat{A}=\widehat{C}\) nên tam giác ABC cân tại B

\( \Rightarrow BA = BC\)

Áp dụng định lí tổng 3 góc trong tam giác ABC, có:

\( \Rightarrow \widehat B = {180^o} - {100^0} = {80^o}\)

\( \Rightarrow \widehat B > \widehat A=\widehat C\)

\( \Rightarrow AC\) là cạnh lớn nhất tam giác ABC (Quan hệ giữa góc và cạnh đối diện trong tam giác)

c=60

a=80

b=40

a>c>b

Ta có:

\(\widehat{A}>\widehat{B}=\widehat{C}\left(90^0>45^0=45^0\right)\)

`@` Theo định lý quan hệ giữa góc và cạnh đối diện

`->`\(\text{BC > AC = AB}\).

thôi nha mik tự làm đc r

Ta thấy AC = 4 cm; A’C’ = 4 cm.

Vậy AC = A’C’.

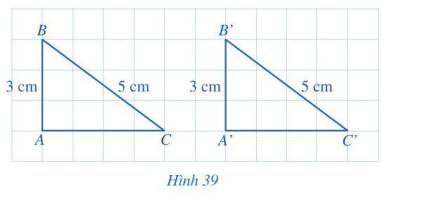
Xét hai tam giác vuông: ∆ABC và ∆A'B'C' có:

BC = B'C' = 5 cm

AB = A'B' = 3 cm

⇒ ∆ABC = ∆A'B'C' (cạnh huyền - cạnh góc vuông)

⇒ AC = A'C' (hai cạnh tương ứng)

Tham khảo:

a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)

Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)

b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>(\widehat {BAK}=90^0\)

Xét tam giác BCK, ta có :

\(\widehat {BKC} > {90^o} > \widehat {BCK}\)

\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)