Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABDABD cân tại BB nên ˆBAK=180o−ˆABD2BAK^=180o−ABD^2
⇒ˆABK=45o−ˆB2⇒ˆAKC=ˆABC+ˆBAK=45o+ˆB2⇒ABK^=45o−B^2⇒AKC^=ABC^+BAK^=45o+B^2
ˆKAC=90o−(45o−ˆB2)=45o+ˆB2KAC^=90o−(45o−B^2)=45o+B^2
⇒ˆAKC=ˆKAC⇒ΔAKC⇒AKC^=KAC^⇒ΔAKC cân tại C
Tương tự ta cũng có ΔBALΔBAL cân tại B.
b) Áp dụng định lý ta - lét ta có :
IGHG=IGKC.BDHG.KCBD=DGDC.DCCG.ACAB=ABAC.ACAB=1IGHG=IGKC.BDHG.KCBD=DGDC.DCCG.ACAB=ABAC.ACAB=1
⇒IG=HG⇒⇒IG=HG⇒ tam giác IHGIHG vuông cân.
Chứng minh tương tự cũng có tam giác IGJIGJ vuông cân.
⇒ΔIHJ⇒ΔIHJ là tam giác vuông cân.
Hình gửi kèm
mình ghi nhanh quá mình ghi lộn b) \(\frac{IG}{HG}=\frac{IG}{HC}.\frac{BD}{HG}.\frac{KC}{BD}=\frac{DG}{DC}.\frac{DC}{CG}.\frac{AC}{AB}=\frac{AB}{AC}.\frac{AC}{AB}=1\)

1c (2 câu kia em tự giải)
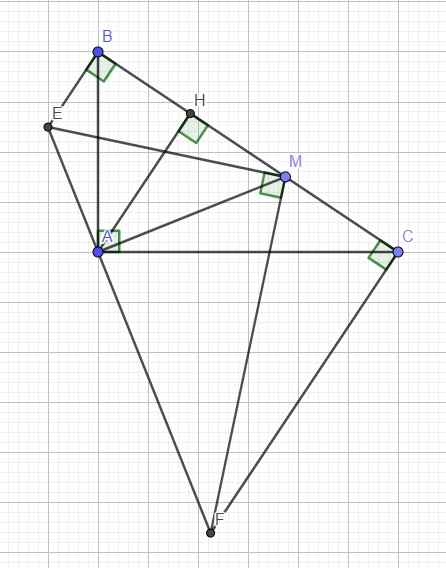
Kẻ đường cao AH \(\Rightarrow\) AH cố định
Do \(\widehat{MAF}\) và \(\widehat{MCF}\) cùng nhìn MF dưới 1 góc vuông nên tứ giác MAFC nội tiếp
\(\Rightarrow\widehat{AFM}=\widehat{ACM}\) (cùng chắn AM)
\(\Rightarrow\Delta_VFME\sim\Delta_VCAB\left(g.g\right)\) với tỉ số đồng dạng \(k=\dfrac{AM}{AH}\)
\(\Rightarrow S_{MEF}=k^2.S_{ABC}\Rightarrow S_{MEF-min}\) khi \(k_{min}\)
Mà trong tam giác vuông AHM ta có \(AH\le AM\Rightarrow k\ge1\Rightarrow k_{min}=1\) khi M trùng H
Hay diện tích MEF min khi M là chân đường cao từ A xuống BC



Chú ý ghi lời giải, không khi đáp số !