Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AH=(BC.1/2)tan60 ct lương giác
=BC.tan60.1/2=\(\sqrt{3}\)/2
họk tốt!

a: \(\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\)
b: lấy điểm H sao cho \(\overrightarrow{AH}=\overrightarrow{GC}\)
\(\overrightarrow{AH}=\overrightarrow{GC}\)
=>AH//GC và AH=GC
Xét tứ giác AHCG có
AH//CG
AH=GC
Do đó: AHCG là hình bình hành
ΔABC đều có G là trọng tâm
nên \(AG=GB=GC=\dfrac{a\sqrt{3}}{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AH}\right|\)
\(=\left|\overrightarrow{HA}+\overrightarrow{AB}\right|=\left|\overrightarrow{HB}\right|=HB\)
AHCG là hình bình hành
=>HC=AG và HC//AG
=>\(HC=\dfrac{a\sqrt{3}}{3}\)
ΔABC đều có G là trọng tâm
nên GB=GC=GA
GB=GC
AB=AC
Do đó: AG là đường trung trực của BC
=>AG\(\perp\)BC
mà CH//AG
nên CH\(\perp\)CB
=>ΔCHB vuông tại C
=>\(BH^2=HC^2+BC^2\)
=>\(BH^2=\left(\dfrac{a\sqrt{3}}{3}\right)^2+a^2=a^2+\dfrac{1}{3}a^2=\dfrac{4}{3}a^2\)
=>\(BH=a\cdot\dfrac{2\sqrt{3}}{3}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=BH=\dfrac{2a\sqrt{3}}{3}\)

+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)

+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
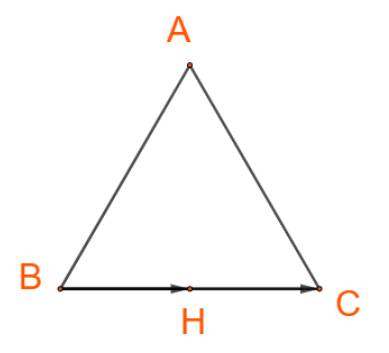
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
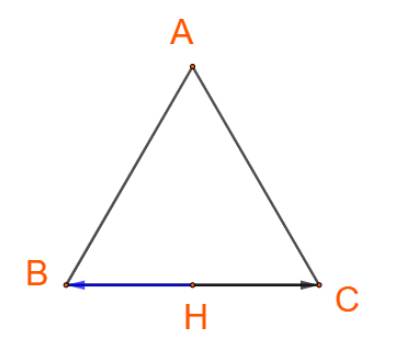

Theo tính chất trọng tâm tam giác ta luôn có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\Rightarrow\overrightarrow{GA}=-\overrightarrow{GB}-\overrightarrow{GC}\)
Thế vào đẳng thức giả thiết ta được:
\(BC.\left(-\overrightarrow{GB}-\overrightarrow{GC}\right)+AC.\overrightarrow{GB}+AB.\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow\left(AC-BC\right)\overrightarrow{GB}=\left(BC-AB\right)\overrightarrow{GC}\) (1)
Mà \(\overrightarrow{GB};\overrightarrow{GC}\) không phải 2 vecto cùng phương
\(\Rightarrow\left(1\right)\) xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}AC-BC=0\\BC-AB=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AC=BC\\AB=BC\end{matrix}\right.\)
\(\Rightarrow AB=AC=BC\) \(\Rightarrow\Delta ABC\) là tam giác đều

Gọi M là trung điểm của BC
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
\(\Leftrightarrow\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)

Gọi M là trung điểm của BC
Ta có: ΔABC đều
mà AM là đường trung tuyến
nên AM\(\perp\)BC tại M
Xét ΔAMB vuông tại M có \(sinB=\dfrac{AM}{AB}\)
=>\(\dfrac{AM}{1}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AM=\dfrac{\sqrt{3}}{2}\)
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
=>\(\overrightarrow{AB}-\overrightarrow{CA}=2\cdot\overrightarrow{AM}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{CA}\right|=2\cdot AM=2\cdot\dfrac{\sqrt{3}}{2}=\sqrt{3}\)
=>A đúng, B và C đều sai
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)
\(=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=1\)
=>D sai
Kẻ trung tuyến AM, BN
a, \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AM}\right|=2AM\)
\(=2\sqrt{AB^2-\frac{1}{4}BC^2}=2\sqrt{a^2-\frac{1}{4}a^2}=\sqrt{3}.a\)
b, \(\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=\left|-2\overrightarrow{AN}\right|=2AN=\sqrt{3}.a\)
c, \(\left|\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|2\overrightarrow{GM}\right|=\left|\frac{2}{3}\overrightarrow{AM}\right|=\frac{2}{3}AM=\frac{2}{3}.\frac{\sqrt{3}}{2}a=\frac{\sqrt{3}}{3}a\)
d, \(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=CB=a\)