Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là trọng tâm tam giác
\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(=\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là chân đường vuông góc hạ từ G xuống BC hay M là trung điểm BC
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=3MG=AM=\dfrac{a\sqrt{3}}{2}\)

Để chứng minh rằng ama + bmb + cmc ≥ √32, ta sử dụng bất đẳng thức tam giác. Bất đẳng thức tam giác cho biết rằng tổng độ dài của ba đường trung tuyến của một tam giác luôn lớn hơn hoặc bằng bình phương độ dài cạnh tương ứng. Vì vậy, ta có:
ama + bmb + cmc ≥ (ma + mb + mc)²/3
Theo định lý đường trung tuyến, ta biết rằng ma + mb + mc = 3/2(a + b + c). Thay vào biểu thức trên, ta có:
ama + bmb + cmc ≥ (3/2(a + b + c))²/3
Simplifying the expression, we get:
ama + bmb + cmc ≥ 3/4(a + b + c)²
Để chứng minh rằng ama + bmb + cmc ≥ √32, ta cần chứng minh rằng 3/4(a + b + c)² ≥ √32. Tuy nhiên, để chứng minh điều này, cần thêm thông tin về giá trị của a, b, c.

38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG

\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=a\) (a>0 mới đúng, độ dài ko thể nhỏ hơn 0)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=a\)
\(\Leftrightarrow3\left|\overrightarrow{MG}\right|=a\) (do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\))
\(\Leftrightarrow MG=\dfrac{a}{3}\)
\(\Rightarrow\) Tập hợp M là đường tròn tâm G bán kính \(\dfrac{a}{3}\)


Đáp án A
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
Phương trình đường tròn tâm D qua A; B là:
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
+ M nằm trên đường tròn (1) nên :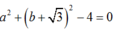
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.