Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta\)ABC cân, mà AF là đường cao
=> AF là đường trung tuyến ( định lý )
=> BF=CF
Xét \(\Delta\) BFH và \(\Delta\) CFH có: \(\left\{{}\begin{matrix}BF=CF\\F_1=F_2=90^o\\FH\end{matrix}\right.\)
=> \(\Delta\) BFH = \(\Delta\) CFH (c.g.c)
=> BH=CH ( 2 cạnh tương ứng )
=> \(\Delta\) BHC là tam giác cân ( định lý )

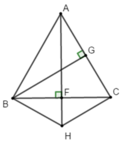
+ Xét tam giác ABF và tam giác ACF đều vuông tại F có:
AB = AC (tam giác ABC đều)
AF: cạnh chung
Do đó: Δ A B F = Δ A C F (cạnh huyền – cạnh góc vuông)
Suy ra: BF = CF (hai cạnh tương ứng)
+ Xét hai tam giác BFH và CFH cùng vuông tại F có:
FH cạnh chung
BF = CF (cmt)
Do đó: Δ B F H = Δ C F H (hai cạnh góc vuông)
Suy ra: CH = BH (hai cạnh tương ứng)
⇒ Δ H B C cân tại H
+ Ta có: B C G ^ + G B C ^ = 90 ° (tam giác BCG vuông tại G)
Mà B C G ^ = B C A ^ = 60 ° (tam giác ABC đều)
Nên G B C ^ = 90 ° − B C G ^ = 90 ° − 60 ° = 30 °
+ Lại có: BG // CH (gt) ⇒ H C B ^ = G B C ^ = 30 ° (hai góc so le trong)
Tam giác HBC cân tại H có góc ở đáy H C B ^ = 30 ° nên Δ H B C không thể là tam giác vuông cân và tam giác đều.
Vậy A, B, C sai, D đúng
Chọn đáp án D

`Answer:`

a. Theo giả thiết: EI//AF
`=>\hat{EIB}=\hat{ACB}=\hat{ABC}=\hat{EBI}` (Do `\triangleABC` cân ở `A`)
`=>\triangleEBI` cân ở `E`
`=>EB=EI`
b. Theo giải thiết: BE=CF=>EI=CF`
Xét `\triangleOEI` và `\triangleOCF:`
`EI=CF`
`\hat{OEI}=\hat{OFC}`
`\hat{OIE}=\hat{OCF}`
`=>\triangleOEI=\triangleOFC(g.c.g)`
`=>OE=OF`
c. Ta có: `KB⊥AB` và `KC⊥AC`
`=>KB^2=KA^2-AB^2=KA^2-AC^2=KC^2`
`=>KB=KC`
Mà `BE=CF`
`=>KE^2=KB^2+BE^2=KC^2+CF^2=KF^2`
`=>KE=KF`
`=>\triangleEKF` cân ở `K`
Mà theo phần b. `OE=OF=>O` là trung điểm `EF`
`=>OK⊥EF`

góc ABD+góc ADB=90 độ
góc EBD+góc EDB=90 độ
mà góc ABD=góc EBD
nên góc ADB=góc EDB
=>góc HDB=góc HBD
=>ΔHBD cân tại H

4,
a/ tgiác ACD và tgiác AME là hai tgiác vuông tại A.
AD = AE (gt)
góc(ADC) = góc (AEM) (góc có cạnh tương ứng vuông góc)
=> tgiácACD = tgiácAME (g.c.g)
b/ ta có: AG//EH (cùng vuông góc với CD)
=> AG // IH
mà gt => AI // GH
vậy AGHI là hình bình hành
=>AG = IH.
mặt khác theo cm trên ta có: tgiác ACD = tgiác AME
=> AM = AC = AB
=> A là trung điểm BM, mà AI // BC
=> AI là đường trung bình của tgiác MBH
=> I là trung điểm của MH.
vậy: IM = IH = AG
có: AM = AB
góc BAG = góc AMI (so le trong)
=> tgiác AGB = tgiác MIA ( c.g.c)
c/ có AG//MH, A là trung điểm BM
=> AG là đường trung bình của tgiácBMH
=> G là trung điểm BH
hay BG = GH.

Chọn D