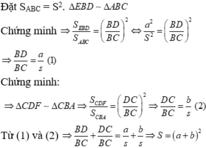Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEMF có
AE//MF
AF//ME
góc EAF=90 độ
Do đó: AEMF là hình chữ nhật
b: \(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=3\cdot4=12\left(cm^2\right)\)

Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
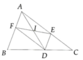

a: MD//AC
=>góc MDB=góc ACB
=>góc MDB=60 độ
Xét tứ giác BEMD có
EM//BD
góc B=góc MDB
=>BEMD là hình thang cân
ME//BC
=>góc AEM=góc ABD=60 độ
Xét tứ giác AEMF có
MF//AE
góc A=góc MEA
=>AEMF là hình thang cân
MF//AE
=>góc CFM=góc CAB=60 độ
Xét tứ giác DCFM có
DM//FC
góc DCF=góc MFC
=>DCFM là hình thang cân
b: Sửa đề: Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của tam giác nào
AEMF là hình thang cân
=>AM=EF
BEMD là hình thang cân
=>BM=ED
FMDC là hình thang cân
=>MC=FD
=>Độ dài 3 cạnh MA,MB,MC bằng độ dài 3 cạnh của ΔEFD

434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!

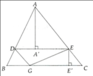
a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)