a)Theo đề: BC/B'C'=10/5=1/2

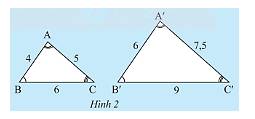
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:

\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)

b) Ta có:

\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).

Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)

a: góc A=góc A'; góc B=góc B'; góc C=góc C'

b: A'B'/AB=A'C'/AC=B'C'/BC

a)   Ta có:   \(\frac{4}{8}=\frac{5}{10}=\frac{6}{12}\left(=\frac{1}{2}\right)\)

hay   \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}\)

\(\Rightarrow\)\(\Delta A'B'C'~\Delta ABC\) 

b)   \(\Delta A'B'C'~\Delta ABC\)

\(\Rightarrow\)\(\frac{P_{A'B'C'}}{P_{ABC}}=\frac{A'B'}{AB}=\frac{8}{4}=2\)

Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !

Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber

vì tam giác ABC đồng dạng với tam giác A'B'C' =>AB/A'B'=BC/B'C'=AC/A'C'

=>BC/B'C'=6/8=3/4=>BC=3.10/4=15/2(cm)

ta lại có AC/A'C'=3/4

=>A'C'/4=AC/3=3/1=3

=>AC=9cm=>A'C'=12(cm)

Vậy BC=15/2 cm ,AC=9cm,A'C'=12cm

Ta có: ABC đồng dạng với tam giác A'B'C' nên ta có:

\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{1}{3}\)(vì \(\frac{AB}{A'B'}=\frac{2}{6}=\frac{1}{3}\)nên 1/3 là tỉ số đồng dạng

hay \(\frac{AC}{A'C'}=\frac{1}{3}\Leftrightarrow\)\(\frac{4}{A'C'}=\frac{1}{3}\Rightarrow A'C'=\frac{4.3}{1}=12\left(cm\right)\)

vậy .....................

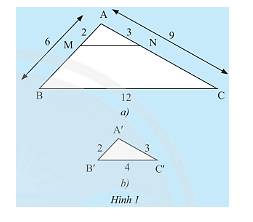
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.

b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)

Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)

Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)

Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).

Vậy \(MN = 4cm\).

c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)

Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:

\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)

Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)

Vì  \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)

Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).