Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là trung điểm của BK
Xét ΔBKC có
M là trung điểm của BC
E là trung điểm của BK
Do đó: ME là đường trung bình
=>ME//KC và ME=KC/2
Xét ΔNME có
A là trung điểm của NM
AK//EM
Do đó K là trung điểm của NE
=>NK=KE=EB
=>NK=1/2KB

Bài 2
gọi E là trung điểm của KB
Vì tam giác CKB có BM=MC ; BE=EK
=>EM//KC
Vì tam giác ENM có AN=AM ; KA//EM
=>EK=KN
Vì KN=KE=EB=>NK=1/2KB

Bài 1:
Xét ΔABC có NQ//BC
nên AN/AB=AQ/AC(1)
Xét ΔABM có NK//BM
nên NK/BM=AN/AB(2)
Xét ΔACM có KQ//MC
nên KQ/MC=AQ/AC(3)
Từ (1), (2) và (3) suy ra NK/BM=KQ/MC
mà BM=MC
nên NK=QK

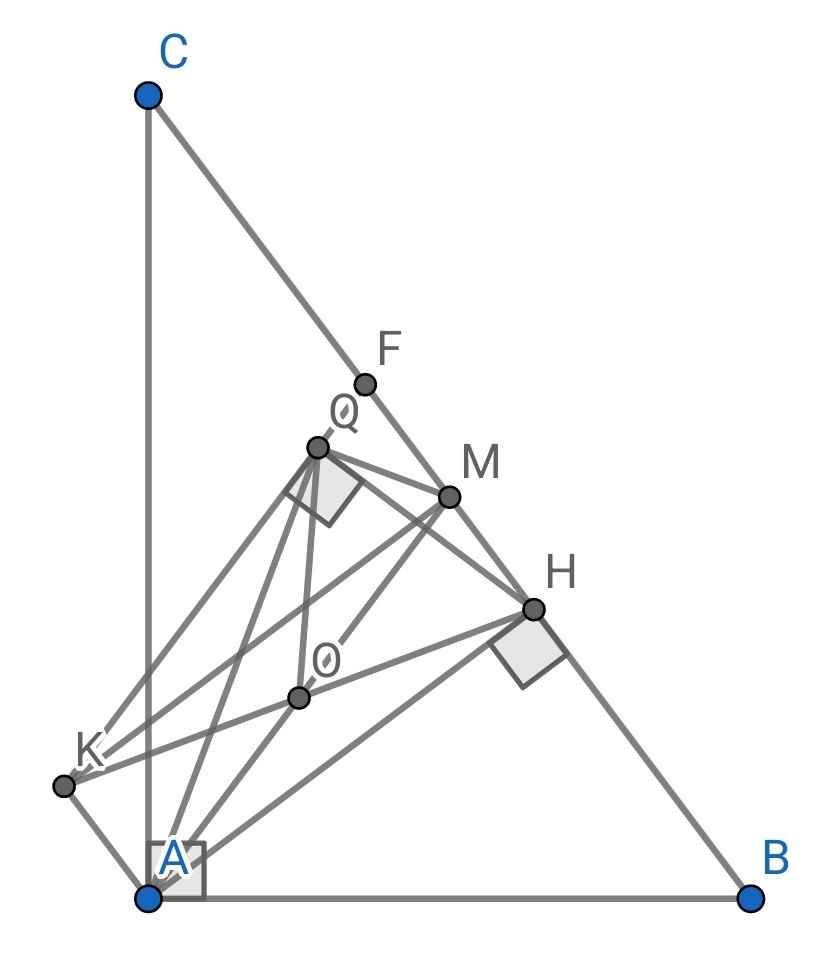 a) Do OH = OK (gt)
a) Do OH = OK (gt)
⇒ O là trung điểm của KH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ AH ⊥ HM
⇒ ∠AHM = 90⁰
Tứ giác AHMK có:
O là trung điểm của AM (gt)
O là trung điểm của KH (cmt)
⇒ AHMK là hình bình hành
Mà ∠AHM = 90⁰ (cmt)
⇒ AHMK là hình chữ nhật
b) Do AHMK là hình chữ nhật (cmt)
⇒ AK = MH và AK // MH
Do MF = MH (gt)
⇒ AK = MF
Do AK // MH (cmt)
⇒ AK // MF
Tứ giác AMFK có:
AK // MF (cmt)
AK = MF (cmt)
⇒ AMFK là hình bình hành
c) Do AHMK là hình chữ nhật (cmt)
⇒ OA = OH = OM = OK = AM : 2
∆HQK vuông tại Q có OQ là đường trung tuyến
⇒ OQ = OH = HK : 2
Mà OH = OM = OA (cmt)
⇒ OQ = OM = OA = AM : 2
∆AQM có:
OQ là đường trung tuyến (do O là trung điểm của AM)
Mà OQ = OA = OM = AM : 2 (cmt)
⇒ ∆AQM vuông tại Q
⇒ MQ ⊥ AQ
Lấy D là điểm đối xứng của C qua A \(\Rightarrow NDMC\)là :
hình bình hành nên nên AD = MC = \(\frac{BC}{2}\) ; ND//BC
Theo định ngĩa Thales : \(\frac{NK}{KB}=\frac{ND}{BC}=\frac{1}{2}\)
Chúc bạn học tốt !!!