Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này có 1 cách cực kì nhanh, ko cần phân tích vecto, đó là sử dụng Menelaus của lớp 8:
Nếu B, K, E thẳng hàng, xét tam giác ACD có BE lần lượt cắt 3 cạnh tam giác tại E, K, B nên theo Menelaus ta có:
\(\frac{EA}{EC}.\frac{BC}{BD}.\frac{DK}{KA}=1\Leftrightarrow\frac{3}{1}.\frac{3}{1}.\frac{DK}{KA}=1\Rightarrow AK=9DK\Rightarrow AK=\frac{9}{10}AD\)
Vậy điểm K nằm ở vị trí sao cho \(\overrightarrow{AK}=\frac{9}{10}\overrightarrow{AD}\) thì B, K, E thẳng hàng

\(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AD}\)
\(=\overrightarrow{BA}+\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{BD}\right)\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{9}\overrightarrow{BC}\)
\(=\dfrac{8}{9}\overrightarrow{BA}+\dfrac{2}{9}\overrightarrow{AC}\)
\(\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AE}=\overrightarrow{BA}+\dfrac{1}{4}\overrightarrow{AC}\)
Vì 8/9:1=2/9:1/4
nên B,E,K thẳng hàng

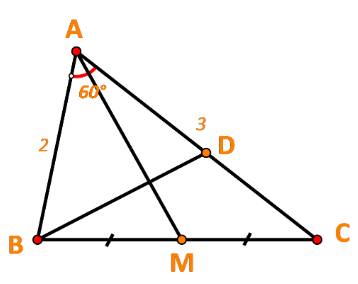
a) \(\overrightarrow {AB} .\overrightarrow {AC} = 2.3.\cos \widehat {BAC} = 6.\cos {60^o} = 3\)
b)
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)(do M là trung điểm của BC)
\( \Leftrightarrow \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \)
+) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} = \frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} \)
c) Ta có:
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {BD} = \left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} } \right)\left( {\frac{7}{{12}}\overrightarrow {AC} - \overrightarrow {AB} } \right)\\ = \frac{7}{{24}}\overrightarrow {AB} .\overrightarrow {AC} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{7}{{24}}{\overrightarrow {AC} ^2} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \\ = - \frac{1}{2}A{B^2} + \frac{7}{{24}}A{C^2} - \frac{5}{{24}}\overrightarrow {AB} .\overrightarrow {AC} \\ = - \frac{1}{2}{.2^2} + \frac{7}{{24}}{.3^2} - \frac{5}{{24}}.3\\ = 0\end{array}\)
\( \Rightarrow AM \bot BD\)