Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MN là đường trung bình của tam giác ABC
\(\Rightarrow\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Từ giả thiết:
\(\overrightarrow{KM}=-2\overrightarrow{KN}=-2\left(\overrightarrow{KM}+\overrightarrow{MN}\right)\)
\(\Rightarrow3\overrightarrow{KM}=2\overrightarrow{NM}\Rightarrow\overrightarrow{KM}=\dfrac{2}{3}\overrightarrow{NM}\)
\(\Rightarrow\overrightarrow{MK}=\dfrac{2}{3}\overrightarrow{MN}=\dfrac{2}{3}\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
Do đó:
\(\overrightarrow{AK}=\overrightarrow{AM}+\overrightarrow{MK}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

\(\overrightarrow{KD}=\overrightarrow{KA}+\overrightarrow{AD}=-\overrightarrow{AK}+\overrightarrow{AD}\)
\(=-\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)+\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\right)+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\)

\(\overrightarrow{CN}=2\overrightarrow{NA}\Leftrightarrow\overrightarrow{CA}+\overrightarrow{AN}=-2\overrightarrow{AN}\)
\(\Leftrightarrow-\overrightarrow{AC}=-3\overrightarrow{AN}\Rightarrow\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}\) (do M là trung điểm AB)
\(\overrightarrow{AK}=\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{4}\\n=\frac{1}{6}\end{matrix}\right.\)

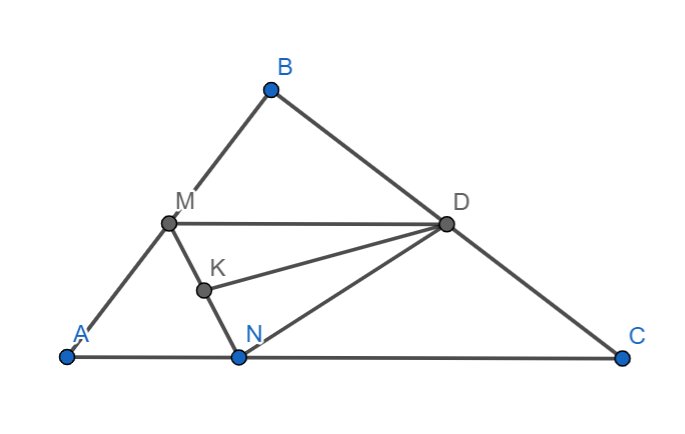
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

\(\overrightarrow{CN}=2\overrightarrow{NA}\Leftrightarrow\overrightarrow{CA}+\overrightarrow{AN}=-2\overrightarrow{AN}\Leftrightarrow\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{AK}=\frac{1}{2}\overrightarrow{AM}+\frac{1}{2}\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\Rightarrow\overrightarrow{KA}=-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(\overrightarrow{KD}=\overrightarrow{KA}+\overrightarrow{AD}=\left(-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\right)+\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{4}\\n=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow m-n=-\frac{1}{12}\)

Bạn xem lại đề, I không thể là trung điểm AC.
Vì I là trung điểm AC, K thuộc AC nghĩa là I, K đều thuộc AC, vậy B,I,K thẳng hàng chỉ khi B cũng thuộc AC nốt (vô lý)
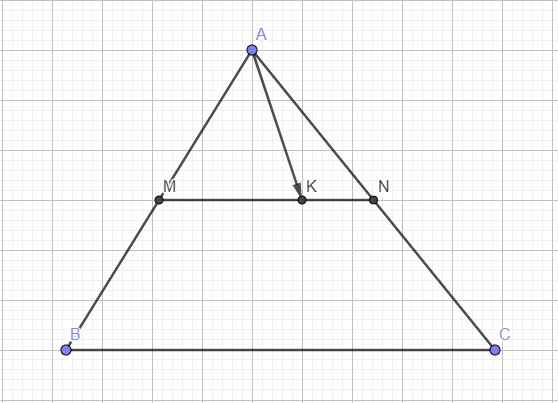
Theo các xác định điểm M, N ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.\)
Theo tính chất trung điểm của MN ta có:
\(\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\).