Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bổ sung đề: Trên tia đối của tia BA, lấy F sao cho BF=EC
a: Xét ΔADB và ΔADE có
AD chung
\(\widehat{DAB}=\widehat{DAE}\)
AB=AE
Do đó: ΔADB=ΔADE
b: AB+BF=AF
AE+EC=AC
mà AB=AE
và BF=EC
nên AF=AC
c: ta có; ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{DBF}=\widehat{DEC}\)
Ta có; ΔABD=ΔAED
=>DB=DE
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC

a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔADB=ΔADE
=>góc ABD=góc AED
b: Xét ΔAEF vuông tại A và ΔABC vuông tại A có
AE=AB
góc AEF=góc ABC
=>ΔAEF=ΔABC
=>AC=AF

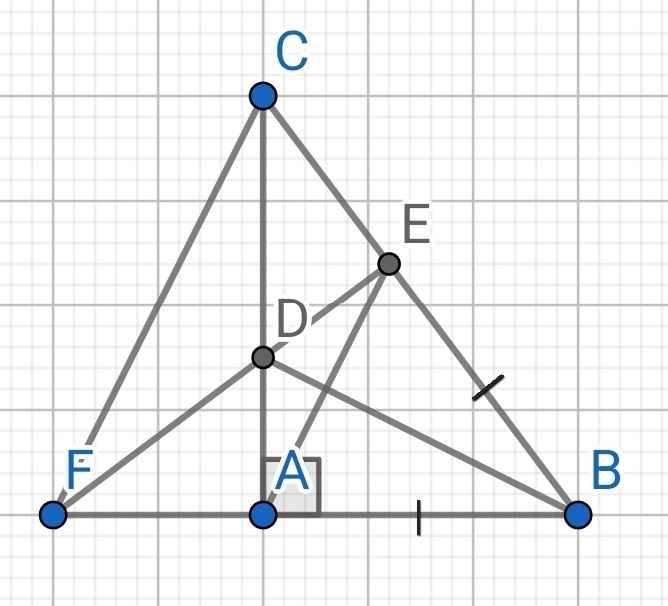 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF