Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEB=góc AHB=90 độ
=>AEHB nội tiếp
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
góc ABH=góc ADC
=>ΔAHB đồng dạng với ΔACD
b: góc HAC+góc AHE
=góc ABE+90 độ-góc HAB
=90 độ
=>HE vuông góc AC
=>HE//CD

a: góc NED+góc NCD=180 độ
=>NEDC nội tiếp
b: ΔAHB vuôg tại H có HM vuông góc AB
nên AM*AB=AH^2
ΔAHC vuông tại H có HN vuông góc AC
nên AN*AC=AH^2
=>AM*AB=AN*AC

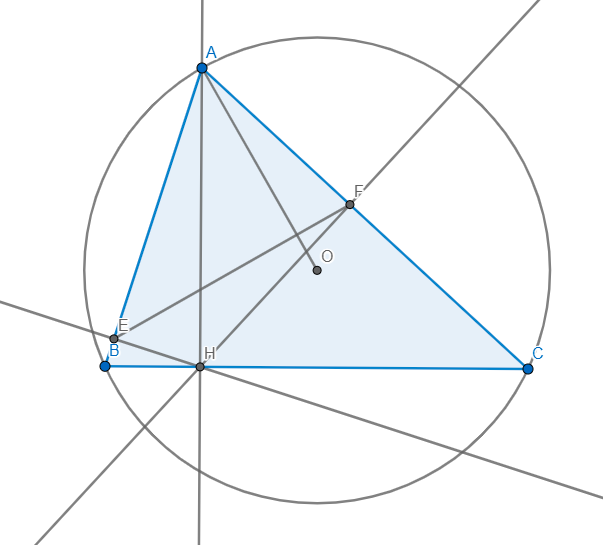
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề
Kẻ tiếp tuyến Ax của đường tròn (O).
Trong tam giác ABH vuông tại H có đường cao HE nên ta có \(AH^2=AE.AB\)
Tương tự, ta cũng có \(AH^2=AF.AC\), từ đó suy ra \(AE.AB=AF.AC\) hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ACB\) có \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\left(cmt\right)\) và \(\widehat{A}\) chung
\(\Rightarrow\Delta AEF~\Delta ACB\left(c.g.c\right)\) \(\Rightarrow\widehat{AEF}=\widehat{ACB}\) (1)
Mặt khác, trong đường tròn (O) có \(\widehat{BAx}\) và \(\widehat{ACB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung, và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\) nên ta có \(\widehat{BAx}=\widehat{ACB}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AEF}=\widehat{BAx}\) \(\Rightarrow EF//Ax\) (2 góc so le trong bằng nhau)
Lại có Ax là tiếp tuyến tại A của (O) nên \(Ax\perp OA\) tại A, dẫn đến \(OA\perp EF\) (đpcm)