Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

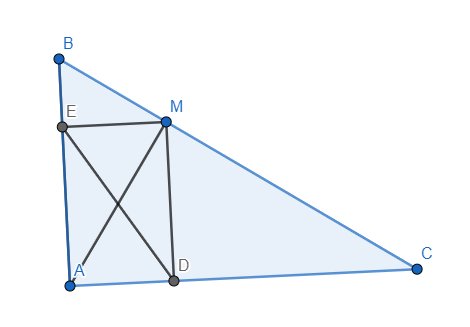
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.

a)tứ giác AEDF là hình chữ nhật (vì E=A=F=900 )
Để tứ giác AEDF là hình vuông thì AD là tia phân giác của góc BAC
b)do tứ giác AEDF là hình chữ nhật nên AD=EF
=>3AD+4EF nhỏ nhất => AD nhỏ nhất
D là hình chiếu góc vuông của A lên BC

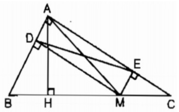
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC