Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao BM:
\(AH^2=AM.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao CN:
\(AH^2=AN.AC\) (2)
(1);(2)\(\Rightarrow AM.AB=AN.AC\)

Trong tam giác AMN, ta có:
MN = AN.sin(∠MAN) (định lí sin)
Vì MN là hình chiếu vuông góc của D lên AB và AC, nên AN = AD.cos(∠BAC) và AM = AD.cos(∠CAB). Thay vào công thức trên, ta có:
MN = AD.cos(∠CAB).sin(∠BAC)
Do đó, để chứng minh MN = AD.sin(BAC), ta cần chứng minh rằng:
cos(∠CAB).sin(∠BAC) = sin(∠BAC)
Áp dụng định lí sin, ta có:
cos(∠CAB).sin(∠BAC) = sin(∠BAC).cos(∠CAB)
Vì cos(∠CAB) = cos(90° - ∠BAC) = sin(∠BAC), nên:
sin(∠BAC).cos(∠CAB) = sin(∠BAC).sin(∠BAC) = sin^2(∠BAC)
Vậy, MN = AD.sin(BAC).
Như vậy, đã chứng minh hai điều kiện trên.

a: Xét ΔABH vuông tại H có HD là đường cao
nên \(BD\cdot BA=BH^2\)
=>\(BA\cdot3,6=6^2=36\)
=>BA=10(cm)
AD+DB=BA
=>AD+3,6=10
=>AD=6,4(cm)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét ΔAHB vuông tại H có HD là đường cao
nên \(HD\cdot AB=HA\cdot HB\)
=>\(HD\cdot10=6\cdot8=48\)
=>HD=4,8(cm)
b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE và ΔACB có
AD/AC=AE/AB
\(\widehat{DAE}\) chung
Do đó: ΔADE đồng dạng với ΔACB

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH
ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>DE*BC=AB*AC

a, Xét tg ABH vuông tại H có đg cao HE
\(AE\cdot AB=AH^2\left(1\right)\)
Xét tg ACH vuông tại H có đg cao HF
\(AF\cdot AC=AH^2\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AE\cdot AB=AF\cdot AC\)
b, Xét tg AEF và tg ACB có
\(AE\cdot AB=AF\cdot AC\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\\ \widehat{A}.chung\)
Do đó \(\Delta AEF\sim\Delta ACB\left(c.g.c\right)\)
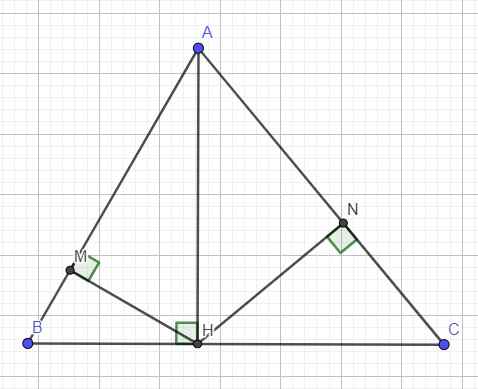
Do M, N lần lượt là hình chiếu của H lên AB, AC
⇒ HM ⊥ AB và HN ⊥ AC
∆AHB vuông tại H có HM là đường cao
⇒ AH² = AM.AB (1)
∆AHC vuông tại C có HN là đường cao
⇒ AH² = AN.AC (2)
Từ (1) và (2) ⇒ AM.AB = AN.AC