Câu a:

Xét tam giác BOD và tam giác COD có

BD=CD (Hai tiếp tuyến cùng xp từ 1 điểm)

OD chung

OB=OC (bán kính (O))

=> tg BOD = tg COD (c.c.c) => ^DOC = ^DOB (1)

Gọi K là giao của OD với (O) ta có 

sđ ^BOD = sđ cung BK; sđ ^COD = sđ cung CK (2)

Từ (1) và (2) => sđ cung BK = sđ cung CK mà sđ cung BK + sđ cung CK = sđ cung BKC => sđ cung BK = sđ cung CK = 1/2 sđ cung BKC (3)

Ta có sđ ^BAC = 1/2 sđ cung BKC (góc nội tiếp) (4)

Từ (2) (3) (4) => ^BAC = ^DOC (dpcm)

Câu 2:

Ta có sđ ^DBC = 1/2 sđ cung BKC (góc giữa tiếp tuyến và dây cung)

sđ ^BAC = 1/2 sđ cung BKC

=> ^BAC = ^DBC (1)

AB//DF => ^BAC = ^DIC (góc đồng vị) (2)

Từ (1) và (2) => ^DBC = ^DIC => B và I cùng nhìn DC dưới hai góc băng nhau => B; D; C; I cùng nawmg trên 1 ffwowngf tròn => tứ giác BDCI nội tiếp

Câu 3:

Ta có

sđ ^COD = sđ cung CK = 1/2 sđ cung BKC (cmt)

sđ ^BAC = 1/2 sđ cung BKC

=> ^COD = ^BAC

mà ^BAC = ^DIC (cmt)

=> ^COD = ^DIC => O và I cùng nhìn CD dưới 2 góc bằng nhau => tứ giác CDOI nội tiếp (1)

Ta có sđ ^OCD = 90 = 1/2 sđ cung OD (góc nội tiếp), mà sđ ^OID = 1/2 sđ cung OD (góc nội tiếp) => ^OID = ^OCD = 90 => IO vuông góc EF => I thuộc đường tròn đường kính OD

Câu 4:

Ta có B; O; C cố định => D cố định => đường tròn đường kính OD cố định

Mà I thuộc đường tròn đường kính OD cố định

=> Khi A chuyển động trên cung BC thì I di chuyển trên đường tròn đường kính OD

a: Xét tứ giác OBDC có \(\widehat{OBD}+\widehat{OCD}=90^0+90^0=180^0\)

nên OBDC là tứ giác nội tiếp

=>\(\widehat{DOC}=\widehat{DBC}\left(1\right)\)

Xét (O) có

\(\widehat{DBC}\) là góc tạo bởi tiếp tuyến BD và dây cung BC

\(\widehat{BAC}\) là góc nội tiếp chắn cung BC

Do đó: \(\widehat{DBC}=\widehat{BAC}\left(2\right)\)

Từ (1),(2) suy ra \(\widehat{DOC}=\widehat{BAC}\)

b: Ta có: DI//AB

=>\(\widehat{CID}=\widehat{CAB}\)(hai góc đồng vị)

mà \(\widehat{CAB}=\widehat{DBC}\)

và \(\widehat{DBC}=\widehat{DOC}\)

nên \(\widehat{CID}=\widehat{COD}\)

=>CIOD là tứ giác nội tiếp

c: ta có: CIOD là tứ giác nội tiếp

=>\(\widehat{OID}=\widehat{OCD}=90^0\)

=>OI\(\perp\)EF tại I

Ta có: ΔOEF cân tại O

mà OI là đường cao

nên I là trung điểm của EF

=>IE=IF

Cho tam giác $ABC$ không có góc tù $(AB<AC)$, nội tiếp đường tròn $(O;R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng $\widehat{MBC}=\widehat{BAC}$ . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.

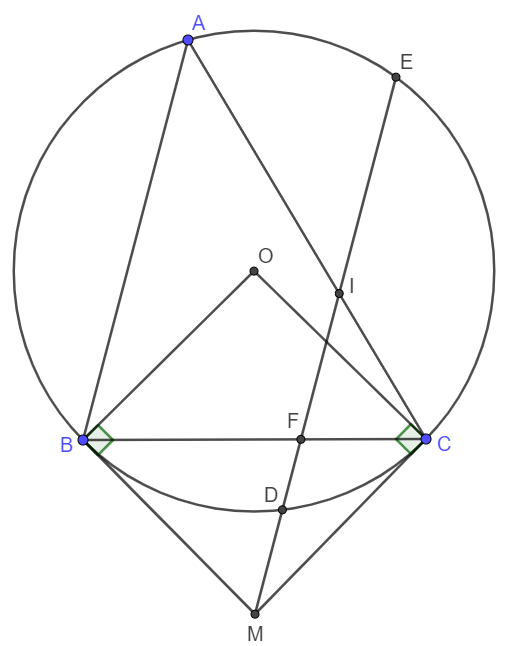
 theo gt, ta co:

goc MBC= BAC (cung chan cung BC)

mat khac, ta lai co goc BAC = MIC ( dong vi)

=> goc MBC= MIC

=> tu giac BICM noi tiep 

đây nha bn

tk cho mk nha

b, Vì DF//AB nên \(\widehat{DHC}=\widehat{BAC}\)(đồng vị)

mà \(\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\widehat{DOC}\)(góc nội tiếp và góc ở tâm)

\(\Rightarrow\widehat{DOC}=\widehat{DHC}\)hay tứ giác DOHC nội tiếp

\(\Rightarrow\widehat{DHO}=\widehat{DCO}=90^0\)\(\Rightarrow OH\perp DF\)

câu c tí nữa làm :P

c, Từ a, b => 5 điểm B,O,H,C,D cùng nằm trên đường tròn đường kính OD

Vì tứ giác BHCD nội tiếp \(\Rightarrow ID.IH=IB.IC\)

Vì tứ giác BECF nội tiếp \(\Rightarrow IE.IF=IB.IC\)

\(\Rightarrow ID.IH=IE.IF\)

a)Xét tứ giác MBOC có 

\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối

\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)

Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

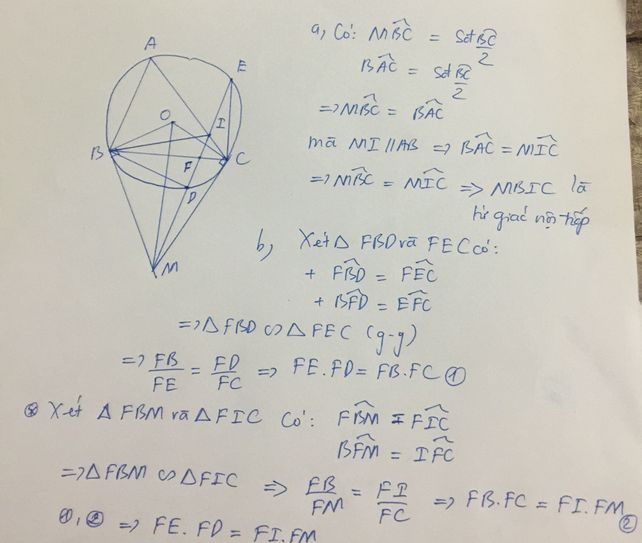
a) Do AB // DE nên \(\widebat{AE}=\widebat{BD}\Rightarrow\widebat{AE}+\widebat{DC}=\widebat{BD}+\widebat{DC}=\widebat{BC}\)

Ta có \(\widehat{MIC}\) là góc có đỉnh nằm trong đường tròn nên \(\widehat{MIC}=\frac{\widebat{AE}+\widebat{DC}}{2}=\frac{\widebat{BC}}{2}\)

Góc \(\widehat{MBC}\) là góc tạo bởi tiếp tuyến và dây cung nên \(\widehat{MBC}=\frac{\widebat{BC}}{2}\)

Suy ra \(\widehat{MIC}=\widehat{MBC}\)

Xét tứ giác BMCI có \(\widehat{MIC}=\widehat{MBC}\) nên BMCI là tứ giác nội tiếp.

b) Ta có \(\widehat{MIC}=\widehat{MBC}\Rightarrow\Delta FIC\sim\Delta FBM\left(g-g\right)\)

\(\Rightarrow\frac{FI}{FB}=\frac{FC}{FM}\Rightarrow FI.FM=FB.FC\)

Ta cũng có \(\widehat{DBF}=\widehat{CEF}\Rightarrow\Delta BFD\sim\Delta EFC\left(g-g\right)\)

\(\Rightarrow\frac{FB}{FE}=\frac{FD}{FC}\Rightarrow FE.FD=FB.FC\)

Vậy nên \(FI.FM=FE.FD\)

c) Do PQ là đường kính nên \(\widehat{PTQ}=90^o\)

Suy ra \(\Delta FIQ\sim\Delta FTM\left(c-g-c\right)\Rightarrow\widehat{FTM}=\widehat{FIQ}\)

Lại có BIMC nội tiếp, BOCM cũng nội tiếp nên 5 điểm B, O, I, C, M cùng thuộc đường trong đường kính OM.

Suy ra \(\widehat{FIQ}=90^o\)

Vậy thì P, T, M thẳng hàng.

d) Ta thấy \(S_{IBC}=\frac{1}{2}BC.d\left(I,BC\right)\)

Do BC không đổi nên S_IBC lớn nhất khi d(I; BC) lớn nhất.

Điều này xảy ra khi I trùng O hay tam giác ABC vuông tại B.

Vậy diện tích tam giác IBC lớn nhất khi AC là đường kính đường tròn (O).

mn ơi giúp mk vs