\(HK=\frac{1}{2}.MN=\frac{1}{4}.AB=3cm\)

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.

b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.

c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)

Tương tự, ta được: EM = (1/2)DC (2)

Từ (1) và (2) Þ DC = 4DI

Xét ΔBDC có 

M là trung điểm của BC

E là trung điểm của DB

Do đó: ME là đường trung bình của ΔBDC

Suy ra: ME//DC 

Xét ΔAME có 

D là trung điểm của AE

DI//EM

Do đó: I là trung điểm của AM

hay AI=IM

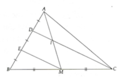
Xét ΔBDC có 

M là trung điểm của BC

E là trung điểm của DB

Do đó: ME là đường trung bình của ΔBDC

Suy ra: ME//DC 

Xét ΔAME có 

D là trung điểm của AE

DI//EM

Do đó: I là trung điểm của AM

hay AI=IM

a: Xét ΔABC có AD/AB=AE/AC

nên DE//BC

b: Xét ΔABI có DM//BI

nên DM/BI=AD/AB

Xét ΔACI có EM//IC

nên EM/CI=AE/AC

=>DM/BI=EM/CI

=>DM=EM

=>M là trung điểm của DE

c: AI là phân giác

=>IB/IC=AB/AC=AD/AE

=>IB*AE=IC*AD

Giải

Ta thấy đường trung bình tam giác ABC nên BEDC là hình thang, lại có\(BM=MC\cdot DN=NC\Rightarrow MN\)   là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì 

\(MI=KN=\frac{DE}{2}\left(1\right)\)

\(MN=\frac{DE^2+BC}{2}\Rightarrow IK=MN-2MI=\frac{DE+BC}{2}-DE\)

\(=\frac{BC-DE}{2}=\frac{DE^2}{2}\left(BC=2DE\right)\left(2\right)\)

\(\Leftrightarrow Q\cdot E\cdot D\Rightarrowđcpm\)

Mình sẽ làm câu b trước rồi từ đó suy ra a
b)Giả sử MP=PQ=QN đã có từ trước
Xét △△ ABC có E là trung điểm AB,D là trung điểm AC \Rightarrow ED là đường trung bình của △△ ABC\Rightarrow ED//BC và ED=BC/2(*)
Xét hình thang EDBC có M là trung điểm BE,N là trung điểm CE \Rightarrow MN//BC( (*) (*) )
Từ (*)( (*) (*) ) \Rightarrow ED//MN
Xét △△ BED có M là trung điểm BE,MP//ED \Rightarrow MP là đường trung bình của △△ BED \Rightarrow MP=ED/2
Tương tự cũng có NQ=ED/2
Ta có :MP=PQ
\Leftrightarrow ED2=BC−ED2ED2=BC−ED2
\Leftrightarrow ED=BC-ED
\Leftrightarrow 2ED=BC
Tương tự với NQ và PQ cũng rứa
Vậy muốn NQ=PQ=MP thì 2ED=BC Điều này là hiển nhiên ở (*)
từ đó phát triển lên câu a)NQ=PQ=MP=1/2ED
\Rightarrow MN=3/2ED \RightarrowMN=3/4BC
Đúng thì thanks giùm nha

a) Xét ΔBCD có

M là trung điểm của BC

E là trung điểm của BD

Do đó: ME là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)

Suy ra: ME//CD và \(ME=\dfrac{CD}{2}\)(Định lí 2 về đường trung bình của tam giác)

b) Xét ΔAEM có 

D là trung điểm của AE

DI//EM

Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)

c) Xét ΔAEM có 

D là trung điểm của AE

I là trung điểm của AM

Do đó: DI là đường trung bình của ΔAEM

Suy ra: DI//EM và \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)

Ta có: \(DI=\dfrac{EM}{2}\)(cmt)

nên \(EM=2\cdot DI\)

\(\Leftrightarrow\dfrac{DC}{2}=2\cdot DI\)

\(\Leftrightarrow DC=4\cdot DI\)

\(\Leftrightarrow DC-DI=4DI-DI\)

\(\Leftrightarrow CI=3DI\)