Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có DN // AB, DM // AC
⇒ ANDM là hình bình hành
⇒ OA = OD hay A và D đối xứng với nhau qua điểm O.
b) D là trung điểm của BC (gt), DM // AC
⇒ M là trung điểm của AB
Tương tự N là trung điểm của AC
Do đó MN là đường trung bình của ΔABC
⇒ MN = (1/2)BC = (1/2).16 = 8cm.

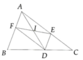
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I

a) Xét tứ giác AEBN:
+ M là trung điểm của AB (gtt).
+ M là trung điểm của EN (N đối xứng E qua M).
=> Tứ giác AEBN là hình bình hành (dhnb).
b) Xét tam giác ABC vuông tại A: AD là trung tuyến (gt).
=> AD = CD = \(\dfrac{1}{2}\) BC (Tính chất đường trung tuyến trong tam giác vuông).
Xét tam giác HEC và tam giác DEA:
+ EC = EA (E là trung điểm của AC).
+ \(\widehat{HEC}=\widehat{DEA}\) (đối đỉnh).
+ \(\widehat{HCE}=\widehat{DAE}\) (AD // HC).
=> Tam giác HEC = Tam giác DEA (c - g - c).
Xét tứ giác ADCH:
+ AD // HC (gt).
+ AD = HC (Tam giác HEC = Tam giác DEA).
=> Tứ giác ADCH là hình bình hành (dhnb).
Mà AD = CD (cmt).
=> Tứ giác ADCH là hình thoi (dhnb).

a: Xét tứ giác AKMN có
MN//AK
AN//MK
Do đó: AKMN là hình bình hành
mà \(\widehat{NAK}=90^0\)
nên AKMN là hình chữ nhật
b: Xét ΔAMQ có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAMQ cân tại A
mà AN là đường cao
nên AN là tia phân giác của góc MAQ(1)
Xét ΔAME có
AK là đường cao
AK là đường trung tuyến
DO đó: ΔAME cân tại A
mà AK là đường cao
nên AK là tia phân giác của góc MAE(2)
Từ (1) và (2) suy ra \(\widehat{QAE}=2\cdot\left(\widehat{MAN}+\widehat{MAK}\right)=2\cdot90^0=180^0\)
hay Q,E,A thẳng hàng

a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM là phân giác của \(\widehat{BAC}\)
Xét tứ giác APMQ có
AP//MQ
AQ//MP
Do đó: APMQ là hình bình hành
Hình bình hành APMQ có AM là phân giác của góc PAQ
nên APMQ là hình thoi
b: Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MQ//AB
Do đó: Q là trung điểm của AC
Xét ΔABC có
P,Q lần lượt là trung điểm của AB,AC
=>PQ là đường trung bình của ΔABC
=>PQ//BC
c: Xét ΔABC có M,Q lần lượt là trung điểm của CB,CA
=>MQ là đường trung bình của ΔABC
=>MQ//AB và \(MQ=\dfrac{AB}{2}\)
mà \(MQ=\dfrac{MD}{2}\)
nên MD=AB
MQ//AB
=>MD//AB
Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
d: Xét tứ giác AMCD có
Q là trung điểm chung của AC và MD
Do đó: AMCD là hình bình hành
Hình bình hành AMCD có \(\widehat{AMC}=90^0\)
nên AMCD là hình chữ nhật
Hình chữ nhật AMCD muốn trở thành hình vuông thì CA là phân giác của góc MCD
=>\(\widehat{ACB}=\dfrac{1}{2}\cdot90^0=45^0\)
a: Xét tứ giác AMDN có
AM//DN
AN//DM
Do đó: AMDN là hình bình hành
=>Hai đường chéo AD và MN cắt nhau tại trung điểm của mỗi đường
hay A và D đối xứng nhau qua O