Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

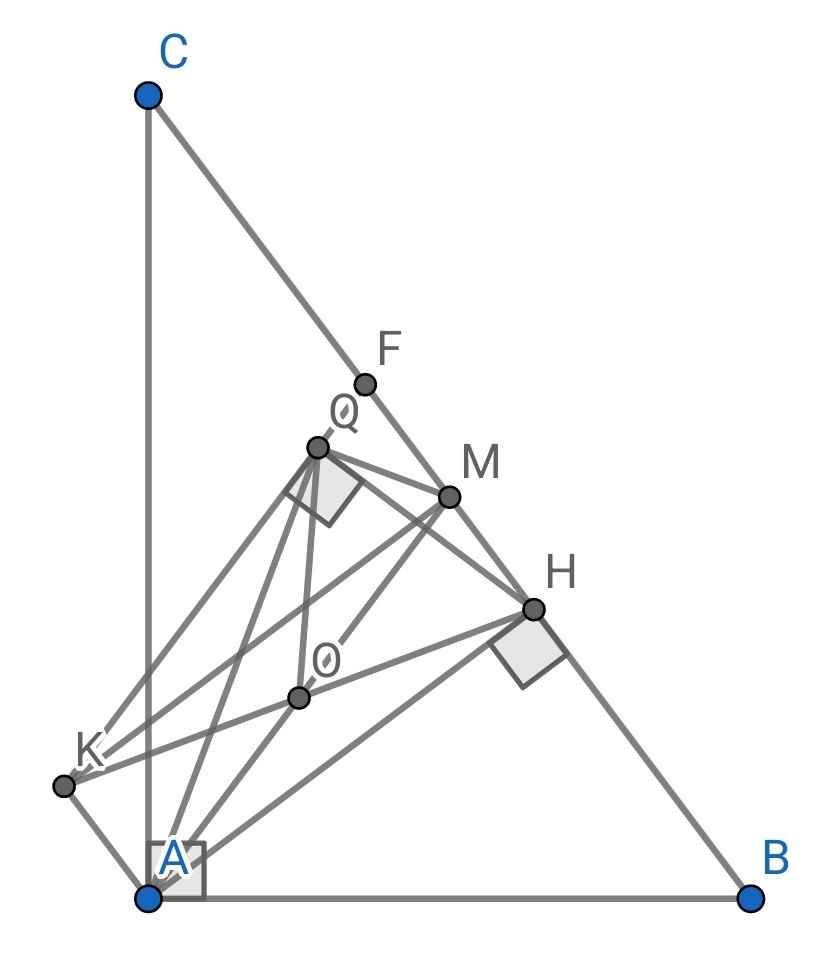 a) Do OH = OK (gt)
a) Do OH = OK (gt)
⇒ O là trung điểm của KH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ AH ⊥ HM
⇒ ∠AHM = 90⁰
Tứ giác AHMK có:
O là trung điểm của AM (gt)
O là trung điểm của KH (cmt)
⇒ AHMK là hình bình hành
Mà ∠AHM = 90⁰ (cmt)
⇒ AHMK là hình chữ nhật
b) Do AHMK là hình chữ nhật (cmt)
⇒ AK = MH và AK // MH
Do MF = MH (gt)
⇒ AK = MF
Do AK // MH (cmt)
⇒ AK // MF
Tứ giác AMFK có:
AK // MF (cmt)
AK = MF (cmt)
⇒ AMFK là hình bình hành
c) Do AHMK là hình chữ nhật (cmt)
⇒ OA = OH = OM = OK = AM : 2
∆HQK vuông tại Q có OQ là đường trung tuyến
⇒ OQ = OH = HK : 2
Mà OH = OM = OA (cmt)
⇒ OQ = OM = OA = AM : 2
∆AQM có:
OQ là đường trung tuyến (do O là trung điểm của AM)
Mà OQ = OA = OM = AM : 2 (cmt)
⇒ ∆AQM vuông tại Q
⇒ MQ ⊥ AQ

a: OK=OH
O nằm giữa K và H
Do đó: O là trung điểm của KH
Xét tứ giác AHMK có
O là trung điểm chung của AM và HK
=>AHMK là hình bình hành
Hình bình hành AHMK có \(\widehat{AHM}=90^0\)
nên AHMK là hình chữ nhật
b: AHMK là hình chữ nhật
=>AK//HM và AK=HM
Ta có: AK//HM
M\(\in\)HF
Do đó: AK//MF
Ta có: AK=MK
MH=MF
Do đó: AK=MF
Xét tứ giác AMFK có
AK//FM
AK=FM
Do đó: AMFK là hình bình hành
c:
Ta có: AHMK là hình chữ nhật
=>AM=HK
ta có: ΔQKH vuông tại Q
mà QO là đường trung tuyến
nên \(QO=\dfrac{KH}{2}=\dfrac{AM}{2}\)
Xét ΔAQM có
QO là trung tuyến
\(QO=\dfrac{AM}{2}\)
Do đó: ΔAQM vuông tại Q
=>QA\(\perp\)QM

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật





