Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

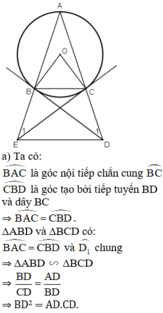
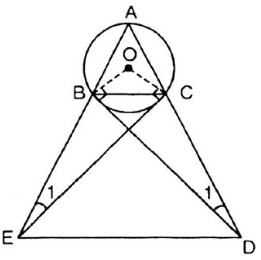
b) ΔABC cân tại A
⇒ AB = AC
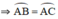
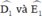 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
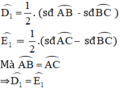
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
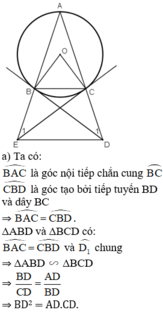
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
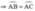
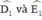 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
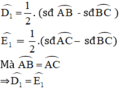
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp

â ) Xét tứ giác BMNC , ta có :
goc BMC = 90o ( gt)
goc BNC = 90o ( gt )
goc BMC = goc BNC = 90o
Vay :tứ giác BMNC nội tiếp ( vì có 2 định M , N cùng nhìn BC dưới một góc 90o )
b) Tứ giác ANHM có : góc ANH = 900 ; góc HMA = 900 (giả thiết)
=> góc ANH + góc HMA = 90 + 90 = 1800
=> Tứ giác ANHM nội tiếp
=> góc AMN = góc ACB (góc ngoài tứ giác nội típ = đối góc trong)
Ta có: góc xAB = góc ACB (nội típ chắn cung AB)
=> góc AMN = góc xAB mà 2 góc ở vị trí so le trong
=> MN // xy
( Hình có bạn vẽ rồi nên mình giải câu b) thui ^^ )

Ai trả lời hộ điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinhanh lênnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn