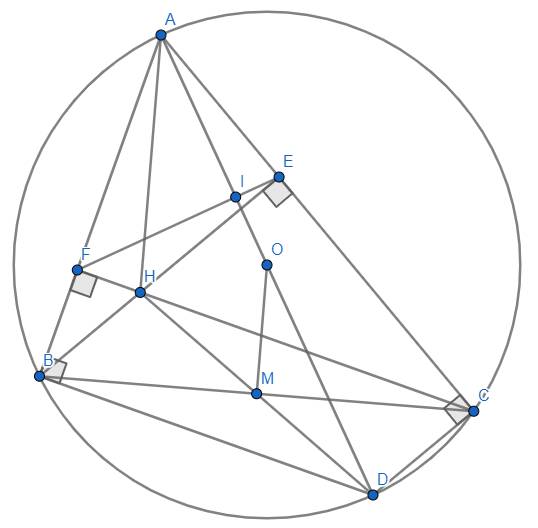
Cho tam giác nhọn ABC nội tiếp trong (O;R) có BD và CE là các đường cao. Cho góc A = 60 độ, tính theo R diện tích tứ giác OEAD

Có thể giải như sau: 
Tam giác vuông ABD có ^BAD = 60o => AD = AB/2 
Dễ thấy tg vuông ABD đồng dạng với tg vuông ACE => AD/AE = AB/AC => AD/AB = AE/AC => tg AED đông dạng tam giác ABC ( vì có chung góc A) => ED/BC = ADAB = 1/2 => ED = BC/2 
Dễ tính được BC = RV3 => ED = RV3/2 
Mặt khác : Vẽ đường kính AF => BF//CE (vì cùng _I_ với AB). Dễ thấy BCDE nội tiếp => ^BDE = ^BCE (cùng chắn cung BE) = ^CBF ( so le trong) = ^CAF (cùng chắn cung CF của (O) ) => AF _I_ DE ( vì đã có AD _I_ BD) 
Vậy S(OEAD) = AO.ED/2 = R^2V3/4 => R = V(4SV3/3)

p/s:tham khảo

a: góc ADH+góc AEH=180 độ

=>ADHE nội tiếp

b: góc EDH=góc BAF

góc FDH=góc ECB

mà góc BAF=góc ECB

nên góc EDH=góc FDH

=>DH là phân giác của góc EDF

a: Xét tứ giác ADHE có

góc AdH+góc AEH=180 độ

=>ADHElà tứ giác nội tiếp

I là trung điểm của AH

b: Xét tứ giác BEDC có

góc BEC=góc BDC=90 độ

=>BEDC là tứ giác nội tiếp

góc EDB=góc BAF

góc FDB=góc ECB
mà góc BAF=góc ECB

nên góc EDB=góc FDB

=>DB là phân giác của góc EDF

và KH/HF=DK/DF đc ko bạn câu b)

Có câu hỏi mà không có ai trả lời vậy

a, xét tứ giác  BCDE có:

góc BEC = 90 độ

góc BDC = 90 độ

=>góc BEC=BDC

=>tứ giác BCDE nt

xét tứ giác ADHE có:

góc AEH = 90 độ

góc ADH=90 độ

=>AEH+ADH=180

=>tứ giác ADHE nt

b,  vì tứ giác EDCB nt(cmt)

=>góc AED=ACB

xet tam giác AED và ACB  có:

góc EAD chung

góc AED=ACB

=>2 tam giác này đồng dạng vs nhau

=>AE/AC=AD/AB

=>AD.AC=AE.AB

C, ta có :góc xAB=ACB

mak góc góc ACB=AED(cmt)

=>góc xAB=AED

=>Ax//ED

mong mọi người kb với mik nhé.yêu nhìu...!!!

a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).

Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).

Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).

b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)

Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)

Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.

Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.

c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)

Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).

Và : \(BE\perp AC\left(gt\right)\)

Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)

Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.

Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)

Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).

Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).

d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).

Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).

Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)

Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)

Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)

\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)

\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)

\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)

\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)

\(\Rightarrow OA\perp EF\) (đpcm).