Gọi M là trung điểm AB \(\Rightarrow\overrightarrow{CG}=\dfrac{2}{3}\overrightarrow{CM}\)

Mà \(\overrightarrow{CM}=\dfrac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\) \(\Rightarrow\overrightarrow{CG}=\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)

Do I là trung điểm AG:

\(\overrightarrow{CI}=\dfrac{1}{2}\overrightarrow{CG}+\dfrac{1}{2}\overrightarrow{CA}=\dfrac{1}{2}\left(\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)+\dfrac{1}{2}\overrightarrow{CA}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)

Câu C: \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\)

Chọn C

a) \(\overrightarrow{BI}=\overrightarrow{BC}+\overrightarrow{CI}=\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}=\overrightarrow{BA}+\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{CA}\)
\(=\overrightarrow{BA}+\overrightarrow{AC}-\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AC}+\overrightarrow{BA}=\dfrac{3}{4}\overrightarrow{AC}-\overrightarrow{AB}\).
b) Có \(\overrightarrow{BJ}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{2}{3}\overrightarrow{AB}=\dfrac{3}{2}\left(\dfrac{1}{2}\overrightarrow{AC}-\overrightarrow{AB}\right)=\dfrac{3}{2}\overrightarrow{BI}\).
Vì vậy 3 điểm B, I, J thẳng hàng.
c)
Trên cạnh AC lấy điểm K sao cho \(\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AC}\).
Tại điểm K dựng điểm T sao cho \(\overrightarrow{KT}=-\dfrac{3}{2}\overrightarrow{AB}=\dfrac{3}{2}\overrightarrow{BA}\).
\(\overrightarrow{BJ}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}=\overrightarrow{AK}+\overrightarrow{KT}=\overrightarrow{AT}\).
Dựng điểm T sao cho \(\overrightarrow{BJ}=\overrightarrow{AT}\).


 

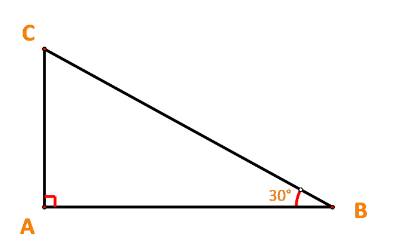
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)

\(\overrightarrow {BA} .\overrightarrow {BC}  = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)

\(\overrightarrow {CA} .\overrightarrow {CB}  = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)

Lời giải:

Kéo dài $AG$ cắt $BC$ tại $M$ thì $M$ là trung điểm $BC$

Ta có:

$\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}+\frac{1}{2}.\overrightarrow{AG}=\overrightarrow{CA}+\frac{1}{2}.\frac{2}{3}.\overrightarrow{AM}$

$=\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AM}$

$=\overrightarrow{CA}+\frac{1}{3}(\overrightarrow{AC}+\overrightarrow{CM})$

$=\overrightarrow{CA}+\frac{1}{3}(-\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB})$

$=\frac{2}{3}\overrightarrow{CA}+\frac{1}{6}\overrightarrow{CB}$

Vậy $m=\frac{2}{3}$

\(a\text{) }\overrightarrow{AB}-\overrightarrow{CD}=\left(\overrightarrow{AC}+\overrightarrow{CB}\right)-\overrightarrow{CD}\\ =\overrightarrow{AC}-\left(\overrightarrow{CD}-\overrightarrow{CB}\right)=\overrightarrow{AC}-\overrightarrow{BD}\)

\(b\text{) }\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BD}+\overrightarrow{CA}=\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)\\ =\left(\overrightarrow{AB}+\overrightarrow{BD}\right)+\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{AD}+\overrightarrow{DA}=0\)

\(c\text{) }\overrightarrow{AC}+\overrightarrow{DE}-\overrightarrow{DC}-\overrightarrow{CE}+\overrightarrow{CB}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DE}-\overrightarrow{DC}\right)-\overrightarrow{CE}\\ =\overrightarrow{AB}+\overrightarrow{CE}-\overrightarrow{CE}=\overrightarrow{AB}\)

\(d\text{) }\overrightarrow{AB}+\overrightarrow{DE}+\overrightarrow{CF}\\ =\left(\overrightarrow{AC}+\overrightarrow{CB}\right)+\left(\overrightarrow{DF}+\overrightarrow{FE}\right)+\left(\overrightarrow{CE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}+\left(\overrightarrow{FE}+\overrightarrow{EF}\right)\\ =\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{CB}+\overrightarrow{DF}\)