Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD

Tham khảo:
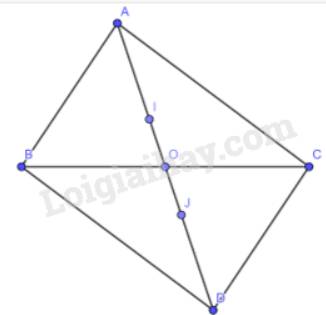
Vì I là trọng tâm tam giác ABC theo giả thiết nên ta có
\(AI = \dfrac{2}{3}AO = 2IO\)(định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
\(DJ = \dfrac{2}{3}OD = 2OJ\) (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
\( \Rightarrow AI = DJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD = 2OI = 2OJ\)
Mà OI = OJ do cùng \( = \dfrac{1}{3}OA = \dfrac{1}{3}OD\)(tính chất trọng tâm trong tam giác)
\( \Rightarrow 2OI = 2OJ = 2\dfrac{1}{3}AO = 2\dfrac{1}{3}OD = IJ\)
\( \Rightarrow AI = DJ = IJ = \dfrac{2}{3}OA = \dfrac{2}{3}OD\)(điều phải chứng minh)

a) Xét tam giác tam giác ABO và tam giác CDO có:
+ \(\text{OB = OD}\) (gt).
+ \(\text{OA = OC }\)(gt).
+ \(\widehat{AOB}\) = \(\widehat{COD}\) (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
=> MO là đường trung bình.
=> MO // BC và MO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> NO là đường trung bình.
=> NO // BC và NO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng = \(\dfrac{1}{2}\) BC).
=> O là trung điểm của MN (đpcm).
a) Xét tam giác tam giác ABO và tam giác CDO có:
+ OB = ODOB = OD (gt).
+ OA = OC OA = OC (gt).
+ ˆAOB���^ = ˆCOD���^ (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do OA = OCOA = OC).
+ O là trung điểm của BD (do OB = ODOB = OD).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do OA = OCOA = OC).
=> MO là đường trung bình.
=> MO // BC và MO = 1212 BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do OB = ODOB = OD).
=> NO là đường trung bình.
=> NO // BC và NO = 1212 BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng = 1212 BC).
=> O là trung điểm của MN (đpcm).

XÉT\(\Delta OAB\)VÀ\(\Delta ODC\)
AO=OD
BO=OC =>\(\Delta OAB=\Delta ODC\left(c-g-c\right)\)
^AOB=^COD
=>^B=^BCD
TA LẠI CÓ ^B + ^ACB=\(90^0\)
=>^BCD + ^ACB=\(90^0\)
XÉT \(\Delta ACP\)VÀ\(\Delta CAB\)
^BAC=^ACD=\(90^0\)
AB=CD =>\(\Delta ACP=\Delta CAB\)(2 CẠNH GÓC VUÔNG)
AC chung
=>BC=AP
vì \(AO=OD=\frac{AD}{2}\)nên \(AO=\frac{BC}{2}\) hay BC=2AO
mk sẽ tích và add cho bạn nào làm đúng và nhanh nhất trong hôm nay thôi nha vì mk đang cần gấp cho ngày mai.

Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)

a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
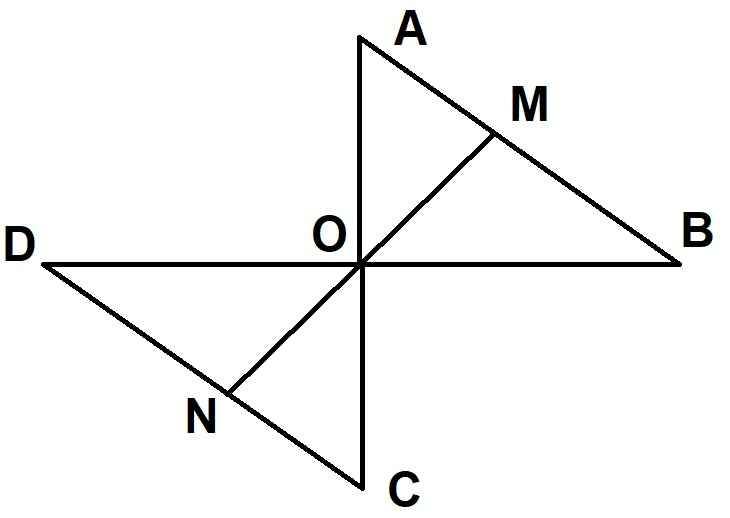
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)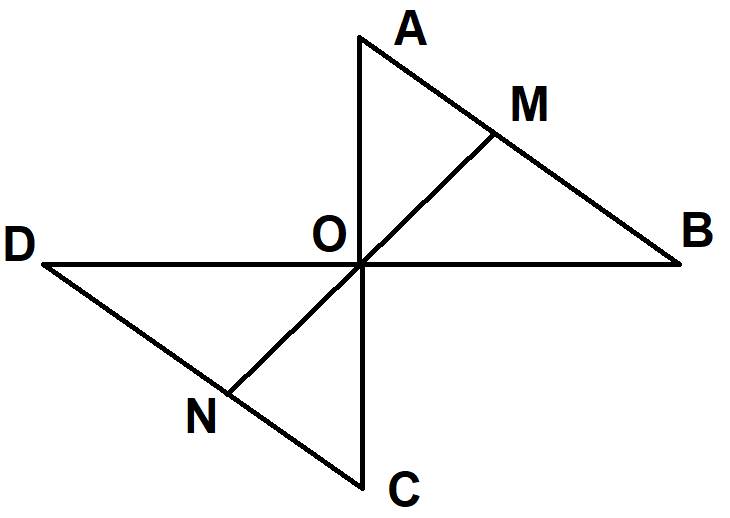

b: Xét tứ giác ABCD có
O là trung điểm của AC
O là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
= 11 nha bn
HG
=11 nha
HT