Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó:MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{16}{2}=8\left(cm\right)\)(1)
hay BMNC là hình thang
b: Xét ΔOBC có
I là trung điểm của OB
K là trung điểm của OC
Do đó: IK là đường trung bình của ΔOBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra MN//IK và MN=IK
hay MNKI là hình bình hành

a) Xét ΔABM và ΔCDM có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔABM=ΔCDM(c-g-c)
b) Ta có: ΔABM=ΔCDM(cmt)
nên \(\widehat{ABM}=\widehat{CDM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{CDM}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
c) Xét ΔDBN có
M là trung điểm của BD(gt)
C là trung điểm của DN(gt)
Do đó: MC là đường trung bình của ΔDBN(Định nghĩa đường trung bình của tam giác)
Suy ra: MC//BN(Định lí 2 đường trung bình của tam giác)
hay BN//AC(đpcm)


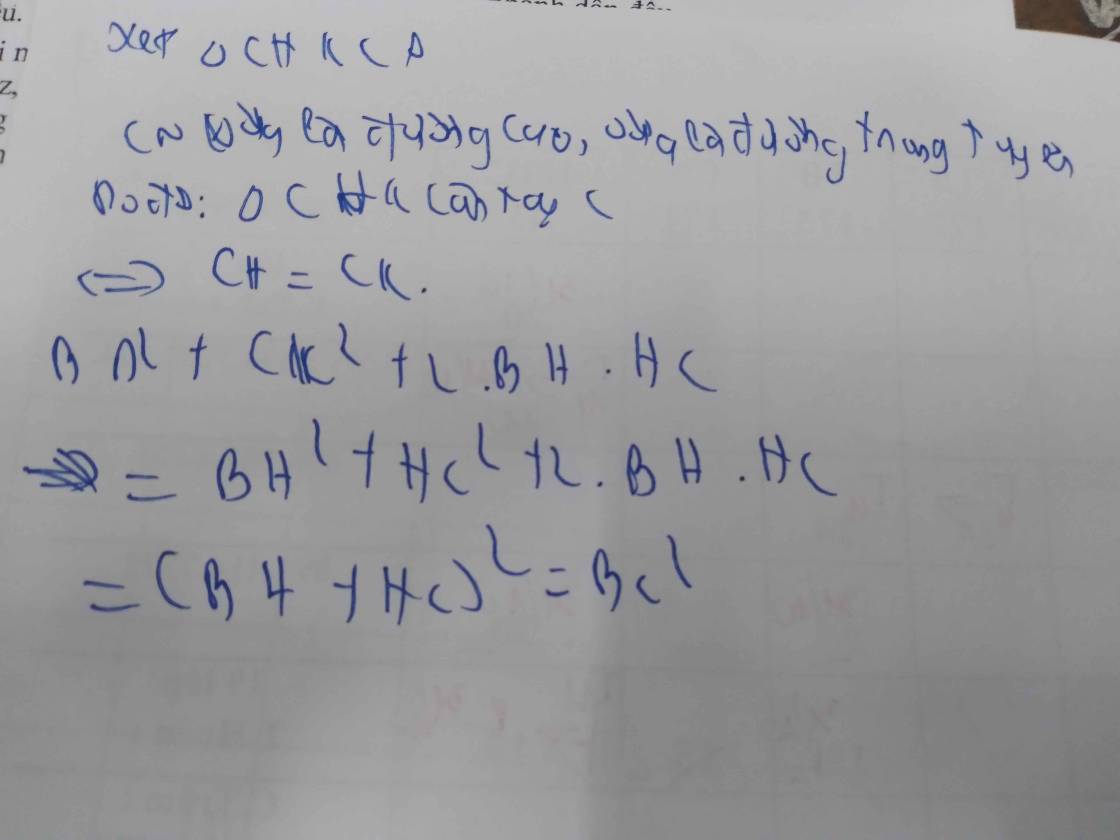
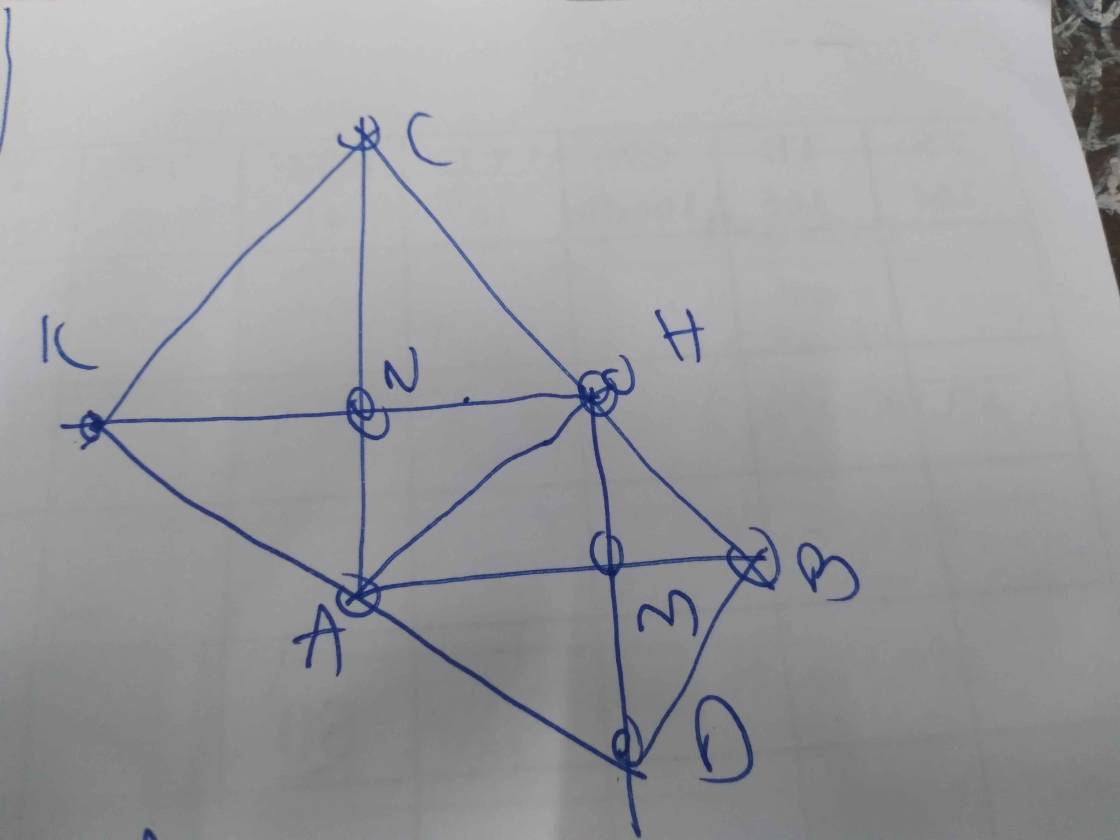
Xét tứ giác AHCB có:
N là trung điểm AC
N là trung điểm BH
=> AHCB là hình bình hành
=> AH//BC và AH=BC(1)
Xét tứ giác AKBC có:
M là trung điểm AB
M là trung điểm CK
=> AKBC là hình bình hành
=> AK//BC và AK=BC(2)
Từ (1),(2)
=> A,K,H thẳng hàng và AK=AH
=> A là trung điểm HK
Cho mình xin hình được không ạ?