Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

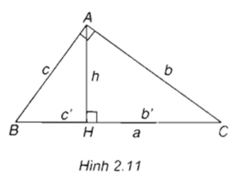
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
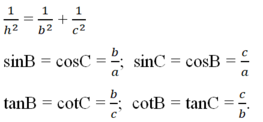

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
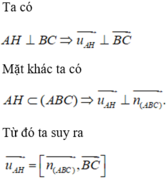
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

Cách làm 2 câu tương tự nhau.
a.
\(\overrightarrow{AB}=\left(2;3\right)\Rightarrow\) đường thẳng AB nhận (3;-2) là 1 vtpt
Phương trình AB (qua A) có dạng:
\(3\left(x-1\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y-1=0\)
\(\overrightarrow{HA}=\left(1;1\right);\overrightarrow{HB}=\left(3;4\right)\)
Do BC vuông góc AH nên nhận (1;1) là 1 vtpt
Phương trình BC (đi qua B) có dạng:
\(1\left(x-3\right)+1\left(y-4\right)=0\Leftrightarrow x+y-7=0\)
Do AC vuông góc HB nên nhận (3;4) là 1 vtpt
Phương trình AC (đi qua A) có dạng:
\(3\left(x-1\right)+4\left(y-1\right)=0\Leftrightarrow3x+4y-7=0\)
Câu b hoàn toàn tương tự

a: vecto AB=(1;-1); vecto AC=(2;1); vecto BC=(1;2)
AB có VTPT là (1;1)
Phương trình AB là;
1(x-1)+1(y+1)=0
=>x+y=0
AC có VTPT là (-1;2)
PT AC là:
-1(x-1)+2(y+1)=0
=>-x+1+2y+2=0
=>-x+2y+3=0
BC có VTPT là (-2;1)
PT BC là;
-2(x-2)+1(y+2)=0
=>-2x+y+6=0
b: AH có VTPT là (1;2)
Phương trình AH là:
1(x-1)+2(y+1)=0
=>x-1+2y+2=0
=>x+2y+1=0

a: \(\overrightarrow{AB}=\left(-11;11\right);\overrightarrow{AC}=\left(-2;6\right)\)
Vì -11/-2<>11/6
nên A,B,C thẳng hàng
ABCD là hình bình hành
=>vecto DC=vecto AB
=>5-x=-11 và 4-y=11
=>x=16 và y=-7
b: \(\overrightarrow{BH}=\left(x+4;y-9\right)\); vecto BC=(9;-5); vecto AH=(x-7;y+2)
Theo đề, ta có:
(x+4)/9=(y-9)/-5 và 9(x-7)+(-5)(y+2)=0
=>-5x-20=9y-81 và 9x-63-5y-10=0
=>-5x-9y=-61 và 9x-5y=73
=>x=481/53; y=92/53
c: Vì (d') vuông góc (d) nên (d'): 4x+3y+c=0
Thay x=-2 và y=3 vào (d'), ta được:
c+4*(-2)+3*3=0
=>c=-1

a.
Gọi tọa độ D có dạng \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;3\right)\\\overrightarrow{DC}=\left(4-x;4-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}4-x=1\\4-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\) \(\Rightarrow D\left(3;1\right)\)
b.
Gọi I là giao 2 đường chéo
Do giao điểm 2 đường chéo hình bình hành là trung điểm AC nên theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_C}{2}=\dfrac{5}{2}\\y_I=\dfrac{y_A+y_C}{2}=\dfrac{5}{2}\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)

Do tam giác ABC có góc B tù và H là chân đường cao của tam giác hạ từ đỉnh A nên điểm B nằm giữa hai điểm H và C.
Do đó, hai vecto B H → ; C H → cùng hướng
Đáp án A

Ta có \(I\left(9;0\right)\) ; \(K\left(0;3\right)\)
\(\overrightarrow{BC}=\left(8;-6\right)=2\left(4;-3\right)\) đường thẳng BC nhận (3;4) là 1 vtpt
Phương trình BC: \(3\left(x-8\right)+4y=0\Leftrightarrow3x+4y-24=0\)
Phương trình đường thẳng AH:
\(4\left(x-9\right)-3\left(y-3\right)=0\Leftrightarrow4x-3y-27=0\)
Tọa độ H: \(\left\{{}\begin{matrix}3x+4y-24=0\\4x-3y-27=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{36}{5};\frac{3}{5}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IH}=\left(-\frac{9}{5};\frac{3}{5}\right)\\\overrightarrow{IK}=\left(-9;3\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{IK}=5\overrightarrow{IH}\Leftrightarrow\) I;K;H thẳng hàng
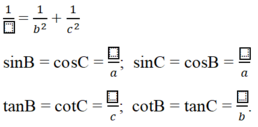

Đáp án B