Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt BC = a, CA = b, AB = c.
Do tam giác ABC vuông tại A nên: \(a^2=b^2+c^2\) (định lý Pytago).
Ta tính được: \(m=\dfrac{a+c-b}{2};n=\dfrac{c+b-a}{2}\).
Từ đó: \(mn=\dfrac{\left(a+c-b\right)\left(c+b-a\right)}{4}=\dfrac{c^2-\left(a-b\right)^2}{4}=\dfrac{\left(a^2+b^2\right)-\left(a-b\right)^2}{4}=\dfrac{ab}{2}=S_{ABC}\).
Vậy...

Lời giải:
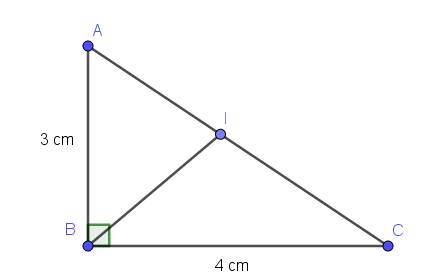
Áp dụng định lý Pitago: $AC=\sqrt{AB^2+BC^2}=\sqrt{3^2+4^2}=5$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{IA}{IC}=\frac{AB}{BC}=\frac{3}{4}$
Mà $IA+IC=AC=5$
$\Rightarrow IA=5:(3+4).3=\frac{15}{7}; IC=5:(3+4).4=\frac{20}{7}$ (cm)

Kẻ CH ⊥ BI và CH cắt BA tại D. Tam giác BCD có BH vừa là phân giác vừa là đường cao => Tam giác BCD cân tại B => BH là đường trung tuyến luôn => CH = DH. và DC = 2HC.
Đặt BC = x() Ta có: AD = BD - AB = BC - AB = x - 5
Gọi giao điểm của AC và BH là E.
Xét tam giác AEB và tam giác HEC có góc EAB = góc EHC = 90độ và góc AEB = góc HEC (đối đỉnh)
=> tam giác AEB ~ tam giác HEC(g.g)
=> Góc HCE = góc ABE.
=> Góc HCE = góc ABC/2 (1)
Mà Góc ECI = gócACB/2 (2)
Từ (1) và (2) => Góc ICH = Góc HCE + Góc ECI = (gócABC + góc ACB)/2 = 90độ/2 = 45độ.
Xét tam giác HIC có góc IHC = 90độ và Góc ICH = 45 độ (góc còn lại chắc chắn = 45 độ)
=> tam giác HIC vuông cân tại H => HI = HC.
Áp dụng đinh lý Py-ta-go cho tam giác này ta được: 2CH² = IC²
=> √2.CH = IC
=> CH = (IC)/(√2)
=> CH = 6/(√2)
=> DC = 2CH = 12/(√2) = 6√2
Xét tam giác: ADC có góc DAC = 90độ
=> Áp dụng định lý Py-ta-go ta có: DC² = AD² + AC²
=> AC² = DC² - AD²
=> AC² = (6√2)² - (x - 5)² (3)
Tương tự đối với tam giác ABC ta có: AC² = BC² - AB²
=> AC² = x² - 5² (4)
Từ (3) và (4) => (6√2)² - (x - 5)² = x² - 5²
<=> 72 - (x² - 10x + 25) = x² - 25
<=> 72 - x² + 10x - 25 - x² + 25 = 0
<=> -2x² + 10x + 72 = 0
<=> x² - 5x - 36 = 0
<=> x² - 9x + 4x - 36 = 0
<=> x(x - 9) + 4(x - 9) = 0
<=> (x - 9)(x + 4) = 0
<=> x - 9 = 0 hoặc x + 4 = 0
<=> x = 9 hoặc x = -4
=> chỉ có giá trị x = -9 là thoả mãn đk x > 5
=> BC = 5cm
b/ Tương tự ta tính được: CH = √5. => IH = √5 (cm)
=> BH = BI + IH = √5 + √5 = 2√5 (cm).
Xét tam giác BHC có góc BHC = 90độ => tính được BC = 5(cm). Kẻ IK ⊥ BC tại K.
Ta có IK = 1/2 đường cao hạ từ đỉnh H của tam giác BHC (chứng minh dựa vào tính chất đường trung bình).
=> IK.BC = S(BHC) = BH.HC/2
<=> IK.5 = 5
=> IK = 1(cm).
Xét tam giác BIK => tính được BK = 2 cm.
Kẻ IF vuông góc với AB => ta chứng minh đựơc BF = BK và AF = IF = IK
=> AB = (2 + 1)=3 (cm)
=> AC = 4cm

a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>\(AD=\dfrac{3}{2}=1,5\left(cm\right)\)
b: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCD}\) chung
Do đó: ΔCHD đồng dạng với ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CD}{CB}\)
=>\(CH\cdot CB=CA\cdot CD\)
c: Ta có: AE\(\perp\)BC
DH\(\perp\)BC
Do đó: HD//AE
Xét ΔAEC có HD//AE
nên \(\dfrac{HC}{HE}=\dfrac{CD}{DA}\)
mà \(\dfrac{CD}{DA}=\dfrac{BC}{BA}\)
nên \(\dfrac{HC}{HE}=\dfrac{BC}{BA}\)
d: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>BA=BH và DA=DH
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: DA=DH
=>D nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra BD là đường trung trực của AH
=>BD\(\perp\)AH tại O và O là trung điểm của AH
=>OA=OH(3)
Xét ΔCMN có AO//MN
nên \(\dfrac{AO}{MN}=\dfrac{CO}{CM}\left(4\right)\)
Xét ΔCBM có OH//BM
nên \(\dfrac{OH}{BM}=\dfrac{CO}{CM}\left(5\right)\)
Từ (3),(4),(5) suy ra MN=BM
=>M là trung điểm của BN