a.

• áp dụng định lí pytago trong tam giác ABC vuông tại A, ta có :

BC^2 = AC^2 + AB^2 

BC^2 = 3^2 + 4^2

BC^2 = 9 + 16

BC^2 = 25

BC = căn bậc 2 của 25

BC = 5 ( cm )

vậy BC = 5 cm

• diện tích của tam giác ABC là :

3 . 4 : 2 = 6 ( cm^2 )

vậy diện tích của tam giác ABC là 6 cm^2

b. xét tam giác HBA và tam giác HAC, ta có :

góc HBA = góc HAC ( hai góc kề bù )

góc A là góc chung ( gt )

do đó: tam giác HBA và tam giác HAC là hai tam giác đồng dạng ( g - g )

c. HA/HB = HC/HA ( cmt )

=> HA^2 = HB . HC

d. vì BD = 1/2BC ( t/chất của đường phân giác trong tam giác vuông )

nên BD = 1/2 . 5 = 2,5 ( cm )

mà BD = DC = 1/2BC

=> DC = 2,5 ( cm )

vậy BC , DC = 2,5 cm

a: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

AH=3*4/5=2,4cm

BH=3^2/5=1.8cm

\(S_{BCA}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)

b Xét ΔHBA vuông tại H và ΔHAC vuông tại H co

góc HBA=góc HAC

=>ΔHBA đồng dạng với ΔHAC

c: ΔHBA đồng dạng với ΔHAC

=>HB/HA=HA/HC

=>HA^2=HB*HC

d: ΔABC có AD là phân giác

=>BD/AB=CD/AC

=>BD/3=CD/4=(BD+CD)/(3+4)=5/7

=>BD=15/7cm; CD=20/7cm

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{B}\) chung

Do đó: ΔABC đồng dạng với ΔHBA

=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)

=>\(BA^2=BH\cdot BC\)

b:ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=12^2+16^2=400\)

=>\(BC=\sqrt{400}=20\left(cm\right)\)

\(BA^2=BH\cdot BC\)

=>\(BH=\dfrac{12^2}{20}=7,2\left(cm\right)\)

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(HA^2+7,2^2=12^2\)

=>\(HA^2=12^2-7,2^2=9,6^2\)

=>HA=9,6(cm)

c: Xét ΔABC có BD là phân giác

nên \(\dfrac{AD}{CD}=\dfrac{BA}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\)

=>\(S_{ABD}=\dfrac{3}{5}\cdot S_{BCD}\)

a, Xét ΔABC và ΔHBA có:

∠BAC chung, ∠BHA=∠BAC (=90^o)

=> ΔABC ∼ ΔHBA (g.g)

b, Áp dụng đ/l Pitago vào △ABC ta có:

BC²=AB²+AC² => BC=√(6²+8²)=10 (cm)

Ta có: S_ABC=\(\dfrac{1}{2}\)AB.AC=\(\dfrac{1}{2}\)AH.BC

=> 6.8=AH.10 => AH=4,8 (cm)

c, Xét △HAB và △HCA có:

∠BHA=∠CHA (=90^o), ∠ABC=∠HAC (cùng phụ ∠BCA)

=> △HAB ∼ △HCA (g.g)

=> \(\dfrac{AB}{AC}=\dfrac{\text{△HAB}}{\text{△HCA}}\)=\(\dfrac{6}{8}\)=\(\dfrac{3}{4}\)

d, AD là đường p/g của △ABC => \(\dfrac{AB}{BD}=\dfrac{AC}{DC}\)=\(\dfrac{AB+AC}{BD+DC}=\dfrac{14}{10}=\dfrac{7}{5}\)

=> \(\dfrac{AB}{BD}=\dfrac{7}{5}\) => \(\dfrac{6}{BD}=\dfrac{7}{5}\) => BD=\(\dfrac{30}{7}\) (cm)

=> \(\dfrac{AC}{DC}\)\(=\dfrac{7}{5}\) => \(\dfrac{8}{DC}=\dfrac{7}{5}\) => DC=\(\dfrac{40}{7}\) (cm)

a)

Xét \(\Delta ABC\) và \(\Delta HBA\) có:

           \(\widehat{B}:chung\)

      \(\widehat{BAC}=\widehat{BHA}\left(=90^o\right)\)

\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)           \(\left(ĐPCM\right)\)

a) Xét ΔHBA và ΔABC có:

^A=^H=90^o

^HAB=^ACB(cùng phụ với ^ABC)

→ ΔHBA∼ΔABC(g.g)

b) Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:

\(BC=\sqrt{20^2+15^2}=25cm\)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC\)

\(\rightarrow AH.BC=AB.AC\)

\(\rightarrow AH=\dfrac{AB.AC}{BC}=12cm\)

c) Xét ΔAHB và ΔCHA có:

^AHB=^CHA=90^o

^HCA=^HAB(cùng phụ với ^ABC)

→ ΔAHB∼ΔCHA(g.g)

\(\rightarrow\dfrac{AH}{HB}=\dfrac{HC}{AH}\left(tươngứng\right)\)

\(\rightarrow AH^2=HB.HC\)

a: ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot21\cdot28=294\left(cm^2\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)

mà \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)

nên \(AH\cdot BC=AB\cdot AC\)

b: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=21^2+28^2=1225\)

=>\(BC=\sqrt{1225}=35\left(cm\right)\)

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

 mà DB+DC=BC=35cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)

=>\(DB=5\cdot3=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)

a)Xét tam giác HAB và tam giác ABC

góc ABC : chung

góc BHA=góc BAC=90^o

Suy ra: tam giác HAB ~ tam giác ABC (g-g)

b)Ta có: tam giác ABC vuông tại A

=>AC²=BC.HC (hệ thức lượng)

c)Ta có: \(BC^2=AB^2+AC^2=15^2+20^2=625\Rightarrow BC=25\left(cm\right)\)

Ta lại có: \(AC^2=BC.HC\left(HTL\right)\Rightarrow HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\left(cm\right)\)

a) Xét ΔHBA và ΔABC có:

∠BHA = ∠BAC = 90⁰ ( GT)

Góc B: Chung

Vậy ΔHBA  ~ ΔABC (g.g)

b) Xét ΔHAC và ΔABC.có:

∠AHC = ∠BAC =90⁰ ( GT)

Góc C : Chung

Vậy ΔHAC ~ ΔABC (g.g)

Suy ra:

c) Áp dụng định lí Pytago cho vuông tại A, ta có:

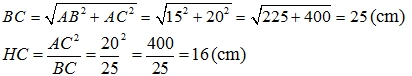
hình vẽ

câu a)