giúp mik vs các bạn ơi

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

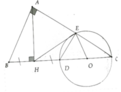
a, Gọi O là trung điểm CD

Từ giả thiết suy ra tam giác ABD và tam giác ODE đều

=> DE = DH = DO = 1 4 BC

=>  H E O ^ = 90 0

=> HE là tiếp tuyến của đường tròn đường kính CD

b, HE = 4 3

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a) Gọi O là trung điểm của CD.

Do E nằm trên đường tròn (O) nên ^DEC=90o hay DE⊥AC.

Thế thì DE//AB.

Gọi M là trung điểm AE, xét hình thang ABDE có: H là trung điểm BD và M là trung điểm AE nên HM là đường trung bình của hình thang.

Vậy nên HM//AB//DE hay HM⊥AE.

Suy ra tam giác HAE cân tại H hay ^HEA=^HAE.

Tam giác OEC cân tại O nên ^OEC=^OCE.

Từ đó ta có: ^HEA+^OEC=^HAE+^OCE=90o.

Suy ra ^OEH=180o−90o=90o.
Vậy nên $HE$ là tiếp tuyến của đường tròn (O).
b) Xét tam giác ABC vuông tại A, áp dụng định lý Pi-ta-go, ta có:

BC=√AB2+AC2=17(cm)

Do tam giác HAE cân tại H nên:

HE = AH = (AB*AC)/BC=120/17

a) Gọi O là trung điểm của CD.

Do E nằm trên đường tròn (O) nên $\widehat{DEC}=90^o$ hay $DE\perp AC$.

Thế thì DE//AB.

Gọi M là trung điểm AE, xét hình thang ABDE có: H là trung điểm BD và M là trung điểm AE nên HM là đường trung bình của hình thang.

Vậy nên HM//AB//DE hay $HM\perp AE.$

Suy ra tam giác HAE cân tại H hay $\widehat{HEA}=\widehat{HAE}$.

Tam giác OEC cân tại O nên $\widehat{OEC}=\widehat{OCE}$.

Từ đó ta có: $\widehat{HEA}+\widehat{OEC}=\widehat{HAE}+\widehat{OCE}=90^o.$

Suy ra $\widehat{OEH}=180^o-90^o=90^o.$
Vậy nên $HE$ là tiếp tuyến của đường tròn (O).
b) Xét tam giác ABC vuông tại A, áp dụng định lý Pi-ta-go, ta có:

$BC=\sqrt{A{B}^2+A{C}^2}=17\left(cm\right)$

Do tam giác HAE cân tại H nên:

HE = AH = $\genfrac{}{}{0ex}{}{AB.AC}{BC}=\genfrac{}{}{0ex}{}{120}{17}.$

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

BAI NAY TUONG DOI DE  NHUNG MINH KHONG BIET VE HINH

bạn cứ giải ra hộ mình đi còn hình thì mình biết vẽ rồi nhé

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD

=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm

=>MD=ME

=>ΔMDE cân tại M

=>góc MED=góc MDE

Xét ΔABD có 

AH vừa là đường cao, vừa là đường trung tuyến

nên ΔABD cân tại A

=>AH là phân giác của góc BAD

=>góc BAH=góc DAH

Xét tứ giác AHDE có

góc AHD+góc AED=180 độ

nên AHDE là tứ giác nội tiếp

=>góc DAH=góc DEH

=>góc DEH=góc BAH=góc C

=>góc MEH=góc C+góc CDE=90 độ

=>HE là tiếp tuyến của (M)

b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)

CD=BC-2x64/17=161/17(cm)

EM=161/17:2=161/34(cm)

MH=MD+DH=BC/2=8,5cm

=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)