Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc AFH=góc AEH=góc FAE=90 độ
=>AEHF là hình chữ nhật
góc JFE=góc JFH+góc EFH
=góc JHF+góc EAH
=góc HBA+góc HAB=90 độ
=>JF là tiếp tuyến của (O)
góc IEF=góc IEH+góc FEH
=góc IHE+góc FAH
=góc HAC+góc HCA=90 độ
=>IE là tiếp tuyến của (O)
=>IE//FJ

\({}\)
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
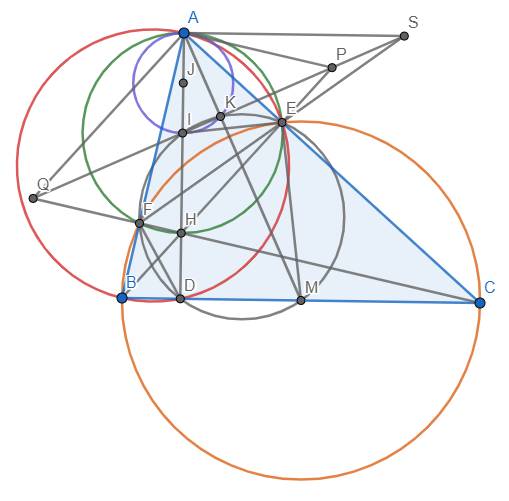
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)

hinh tu ve
cm: aehf la hinh chu nhat vi co 4 goc vuong
suy ra af=eh
\(\Delta BEHdd\Delta BAC\)
\(\frac{EH}{AC}=\frac{BH}{AB}< =>\frac{EH}{BH}=\frac{AC}{AB}\)
tg_bac dd tg_ahc
\(\frac{AC}{AB}=\frac{CH}{AC}\)
suy ra
\(\frac{AF}{BH}=\frac{CH}{AC}\)(do af=eh)
\(\frac{AF}{CH}=\frac{BH}{AC}\)
a. Qua C dung duong thang vuong AC tai C cat NH tai I. De thay tg vuong CAM = tg vuong ICN (AM=CN;goc ACM=goc CIN) =>IC=CA => ACIB la hinh vuong Goi J la trung diem IC. BJ giao NI tai ok De thay BJ // CM => ok la trung diem IH va BK vuong goc IN (Do CM vuong goc IN tai H) => BK vua la duong cao, vua la trung tuyen cua tg BHI =>tg BHIcan tai B =>BH=BI ma ACIB la hinh vuong => BH=BI=BA => ABH can tai B b. De thay tu giac MBIH noi tiep (B=H=ninety) =>goc BIM = goc BHM (cung chan BM) (a million) Mat khac vi HE vuong goc AB => HE // AC => goc EHM = goc ACM (goc dong vi) (2) Hon nua tg AMC = tg BMI => goc BIM = goc ACM (3) Tu (a million), (2), (3) => goc BHM = goc EHM => HM la phan giac goc BHE

a) \(\Delta\)ABC vuông tại A có trung tuyến AO nên ^OAC = ^OCA. Do ^OCA = ^BAH (Cùng phụ ^HAC)
Nên ^OAC = ^BAH = ^ AEF (Do tứ giác AEHF là hcn)
Mà ^AEF + ^AFE = 900 => ^OAC + ^AFE = 900 => OA vuông góc EF (đpcm).
b) Biến đổi tương đương:
\(BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)
\(\Leftrightarrow BE\sqrt{BC.CH}+CF\sqrt{BC.BH}=AB.BC\)(Nhân mỗi vế với \(\sqrt{BC}\))
\(\Leftrightarrow BE\sqrt{AC^2}+CF\sqrt{AB^2}=AB.BC\) (Hệ thức lương)
\(\Leftrightarrow BE.AC+CF.AB=AB.BC\)
\(\Leftrightarrow BH.AH+CH.AH=AB.BC\)(Vì \(\Delta\)EBH ~ \(\Delta\)HAC; \(\Delta\)FHC ~ \(\Delta\)HBA)
\(\Leftrightarrow AH\left(BH+CH\right)=AB.BC\)
\(\Leftrightarrow AH.BC=AB.AC\) (luôn đúng theo hệ thức lượng)
Vậy có ĐPCM.
O là giao của AH và EF
\(AF\perp AB;HE\perp AB\) => AF//HE
\(AE\perp AC;HF\perp AC\) => AE//HF
=> AEHF là hình bình hành mà \(\widehat{A}=90^o\) => AEHF là HCN
\(\Rightarrow AH=EF\) (trong HCN hai đường chéo băng nhau)
\(OA=OH;OE=OF\) (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> OE=OH => tg OEH cân tại O
Vì AEHF là HCN nên
\(\widehat{EAF}=\widehat{EHF}=90^o\) => A và H cùng nhìn EF dưới 1 góc vuông => AEHF là tứ giác nội tiếp đường tròn tâm O bán kính EF
Xét tg vuông BEH có
IB=IH (gt) \(\Rightarrow IE=IB=IH=\dfrac{BH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
=> tg IEH cân tại I \(\Rightarrow\widehat{IEH}=\widehat{IHE}\) (1)
tg OEH cân tại O (cmt) \(\Rightarrow\widehat{OEH}=\widehat{OHE}\) (2)
Mà \(\widehat{IHE}+\widehat{OHE}=\widehat{AHB}=90^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{IEH}+\widehat{OEH}=\widehat{FEI}=90^o\)
\(\Rightarrow IE\perp EF\) mà EF là đường kính (O) => IE là tiếp tuyến đường tròn (O).
C/m tương tự ta cũng có \(JF\perp EF\) => JF cũng là tiếp tuyến với (O)
=> IE//JF (cùng vuông góc với EF)