NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
7
B
14 tháng 4 2017
Áp dụng định lý Py-ta-go vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(18^2+24^2=BC^2\)
\(324+576=BC^2\)
\(BC^2=900=30^2\)
\(\Rightarrow BC=30\left(cm\right)\)
chu vi tam giác ABC là 30+18+24=72(cm)
vậy ...
DT
20 tháng 4 2022
Hình em tự vẽ ra nhé.
Áp dụng đl pytago vào tam giác vuông ABC có:
AB^2 + AC^2 = BC^2
-- > BC = 5 (cm)
Vì tam giác ABC vuông tại A, AM là đường trung tuyến ứng với cạnh huyền BC nên ta có:
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Vì G là trọng tâm tâm giác ABC, ta lại có:
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.2,5=\dfrac{5}{3}\left(cm\right)\)
AH
Akai Haruma
Giáo viên
6 tháng 7
Lời giải:
$AD$ là đường trung tuyến ứng với cạnh huyền $BC$
$\Rightarrow AD=\frac{BC}{2}$
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm)
$\Rightarrow AD=30:2=15$ (cm)
AN
29 tháng 12 2021
Xét tam giác ABC:
BC=EF=5cm
=> Chu vi của tam giác ABC là:
AB+AC+BC=3+4+5=12(cm)
Xét tam giác DEF:
AB=DE=3cm
AC=DF=4cm
=> Chu vi tam giác DEF là:
DE+DF+EF=3+4+5=12
Vậy chu vi tam giác ABC: 12(cm)
Chu vi tam giác DEF:12(cm)
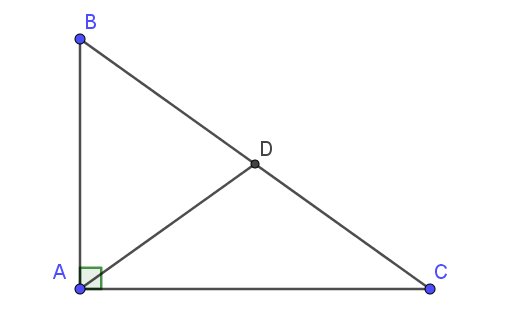
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=30cm\)
Chu vi tam giác ABC là
AB + AC + BC = 72 cm