Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

Vì tam giác ABC vuông nên ta có:

 \(\text{cosB=sinC=0,8}\)

\(\text{cosC=}\)\(\sqrt{1-sin^2C}\) (theo công thức trong SGK ^^)=\(\sqrt{1-0,8^2}=0,6\)

\(tangC=\dfrac{sinC}{cosC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}\left(\approx1,3\right)\)

\(cotangC=\dfrac{cosC}{sinC}=\dfrac{0,6}{0,8}=0,75\)

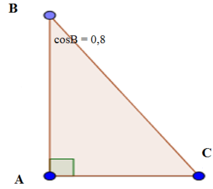
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8

Từ công thức sin2C + cos2C = 1 ta suy ra:

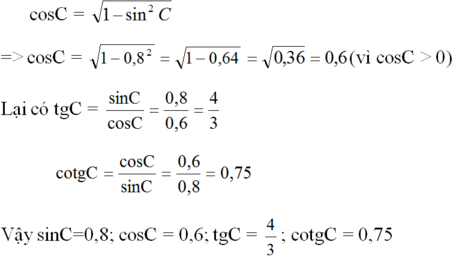
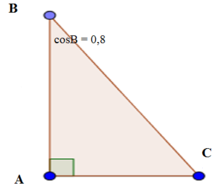
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8

Từ công thức sin2C + cos2C = 1 ta suy ra:

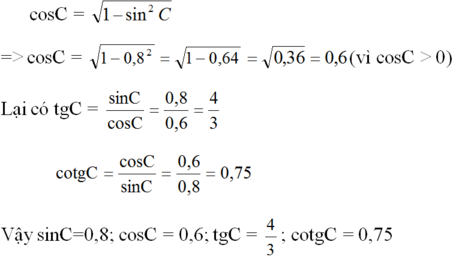
Ta có:

\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB=10.0,8=8\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\)

b.

\(sinC=\dfrac{AB}{BC}=\dfrac{8}{10}=0,8\)

\(cosC=\dfrac{AC}{BC}=\dfrac{6}{10}=0,6\)

\(tanC=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)

\(cotC=\dfrac{AC}{AB}=\dfrac{3}{4}\)

Xét ΔABC vuông tại A ta có:

cos\(\widehat{ABC}\) = sin\(\widehat{ACB}\)

=>sin\(\widehat{ACB}\)=1/3

Xét $\Delta ABC$:

$\cos B=\sin C=0,6$

$\cos^2B=0,6.0,6=0,36$

Mà $\cos^2B+\sin^2B=1$

$\Rightarrow \sin^2B=0,64\\\Leftrightarrow \sinB=0,8(vì\,\,\sinB>0)$

$\Rightarrow \sin B=\cos C=0,8$

Ta có: $\tan C=\dfrac{\sin C}{\cos C}=\dfrac{0,6}{0,8}=0,75$

$\cotC=\dfrac{\cosC}{\sinC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}$

Vậy $\sin C=0,6;\cos C=0,8;\tanC=0,75;\cotC=\dfrac{4}{3}$

Tương tự câu 2