Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBDM vuông tại D và ΔBEM vuông tại E có
BM chung
\(\widehat{DBM}=\widehat{EBM}\)
Do đó: ΔBDM=ΔBEM
b: \(\widehat{DME}=360^0-90^0-90^0-70^0=110^0\)

a) Có tam giác ABC vuông tại A
=>\(BC^2=AC^2+AB^2\) ( định lí Pitago)
=>\(BC^2=8^2+6^2=100\)
=> BC=10 (cm)
b) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
Góc DBA= góc DBK hay góc EBA= góc EBK ( vì BD là tia phân giác của góc ABC)
=> tam giác ABE= tam giác KBE( cạnh góc vuông- góc nhọn)
=> BA=BK ( 2 cạnh tương ứng)
Vạy tam giác ABK cân tại B
c) Nối D với K, ta có tam giác DKE vuông tại E
Theo câu b, ta có tam giác ABE= tam giác KBE
=> KE=EA( 2 cạnh tương ứng) và góc EAB=góc EKB (1)
Xét tam giác vuông DEA và tam giác vuông DEK có
Cạnh DE chung
EA=KE
=> tam giác DEA= tam giác DEK ( 2 cạnh góc vuông)
=> Góc DAE=góc DKE (2)
Từ (1) và (2) =>góc DKE+ góc EKB=góc DAE+ góc EAB= góc DAB=90 độ
=> Góc DKB= 90 độ
Vậy DK vuông góc với BC
d)
Có \(DK⊥BC,AH⊥BC\) =>DK//AB
=> góc DKE= góc EAH (1)
Có tam giác DEA=tam giác DEK
=> góc DAE= góc DKE (2)
Từ (1) và (2) => góc EAH= góc DAE hay góc CAK= góc KAH
Vậy AK là phân giác của góc HAC

Lời giải:
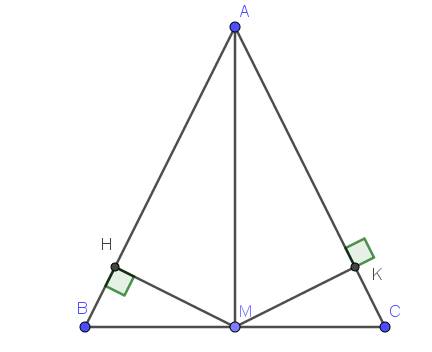
a. Xét tam giác $MHB$ và $MKC$ có:
$\widehat{MHB}=\widehat{MKC}=90^0$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{MBH}=\widehat{MCK}$ (do $ABC$ cân tại $A$)
$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn)
b.
Xét tam giác $MHA$ và $MKA$ có:
$MA$ chung
$\widehat{MHA}=\widehat{MKA}=90^0$
$MH=MK$ (hệ quả từ $\triangle MHB=\triangle MKC$ phần a)
$\Rightarrow \triangle MHA=\triangle MKA$ (ch-cgv)

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là phân giác
nên AM là đường cao
c: Xét ΔAMD vuông tại D và ΔAME vuông tại E có
AM chung
\(\widehat{MAD}=\widehat{MAE}\)
Do đó: ΔAMD=ΔAME
Suy ra: AD=AE



a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
b: Sửa đề: ME cắt BA tại K
Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)
Do đó: ΔBAM=ΔBEM
c: Ta có: ΔBAM=ΔBEM
=>BA=BE
Xét ΔBEK vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBK}\) chung
Do đó: ΔBEK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
d: Ta có: MA+MC=AC
ME+MK=KE
mà AC=KE và MA=ME
nên MK=MC
=>ΔMKC cân tại M
=>\(\widehat{KMC}=180^0-2\cdot\widehat{MKC}\)
mà \(\widehat{KMC}=\widehat{AME}\)(hai góc đối đỉnh)
nên \(\widehat{AME}=180^0-2\cdot\widehat{MKC}\left(1\right)\)
Xét tứ giác BAME có
\(\widehat{BAM}+\widehat{BEM}+\widehat{ABE}+\widehat{AME}=360^0\)
=>\(\widehat{AME}+\widehat{ABC}=180^0\)
=>\(\widehat{AME}=180^0-\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{ABC}=2\cdot\widehat{MKC}\)