làm đc bao nhiêu cũng đc giúp mình với

a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được

\(AB^2+AC^2=BC^2\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=26\left(cm\right)\)

Ta có: \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)

\(\Rightarrow AB.AC=AH.BC\)

\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{120}{13}\left(cm\right)\)

Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H ta đươc:

\(AH^2+HB^2=AB^2\)

\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\frac{50}{13}\left(cm\right)\)

b) Xét tam giác OMN có BC//MN (gt)

\(\Rightarrow\frac{OM}{OC}=\frac{ON}{OB}\)( định lý Ta-let) (1)

Xét tam giác OME có ME// NC ( vì ME//AC )

\(\Rightarrow\frac{OE}{ON}=\frac{OM}{OC}\)( định lý Ta-let) (2)

\(\Rightarrow\frac{ON}{OB}=\frac{OE}{ON}\)

\(\Rightarrow ON^2=OE.OB\left(đpcm\right)\)

a: Xét ΔABC có

M là trung điểm của BC

ME//AC

Do đó: E là trung điểm của AB

Xét ΔABC có

M là trung điểm của BC

MF//AB

Do đó: F là trung điểm của AC

Xét ΔABC có

E là trung điểm của AB

F là trung điểm của AC

Do đó: EF là đường trung bình của ΔABC

b: \(BC=2\cdot EF=2\cdot5=10\left(cm\right)\)

a) Xét tam giác ABC có:

M là trung điểm BC

ME//AC

=> E là trung điểm AB

Xét tam giác ABC có:

M là trung điểm BC

MF//AB

=> F là trung điểm AC

Xét tam giác ABC có:

E là trung điểm AB(cmt)

F là trung điểm AC(cmt)

=> EF là đường trung bình

c) Ta có: EF là đường trung bình

\(\Rightarrow BC=2EF=2.5=10\left(cm\right)\)

a) ∆ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác => MN // BC

Tứ giác MNCB có MN // BC nên là hình thang

b) Xét ∆EQN và ∆KQC có:

     ^ENQ = ^KCQ (BN//CK, so le trong)

     QN = QC (gt)

     ^EQN = ^KQC (đối đỉnh)

Do đó ∆EQN = ∆KQC (g.c.g)

=> EN = KC ( hai cạnh tương ứng)                  (1)

∆NBC có Q là trung điểm của NC và QE // BC nên E là trung điểm của BN => EN = BE              (2)

Từ (1) và (2) suy ra KC = BE

Tứ giác EKCB có KC = BE và KC // BE nên là hình bình hành => EK = BC (đpcm)

c) EF = EQ - FQ = 1/₂BC - 1/₂MN = 1/₂BC - 1/₄BC = 1/₄BC (đpcm)

d) Gọi J là trung điểm của BC 

Ta có EJ là đường trung bình của ∆NBC nên EJ // NC mà FI⊥NC nên FI⊥EJ

Tương tự suy ra EI⊥FJ suy ra I là trực tâm của ∆EFJ => JI⊥EF

Mà dễ thấy EF // BC nên IJ⊥BC

∆BIC có IJ vừa là đường cao vừa là trung tuyến nên là tam giác cân (đpcm)

a) Do M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC.

=> MN //BC

Tứ giác MNCB có MNBC nên MNCB là hình thang.

b) Xét tứ giác EKCB có EK//BC, BE//CK

=> EKCB là hình bình hành

=> EK = BC (đpcm)

dgdsgdsgs

https://hoidap247.com/cau-hoi/27753

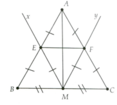
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).

Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;

b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.