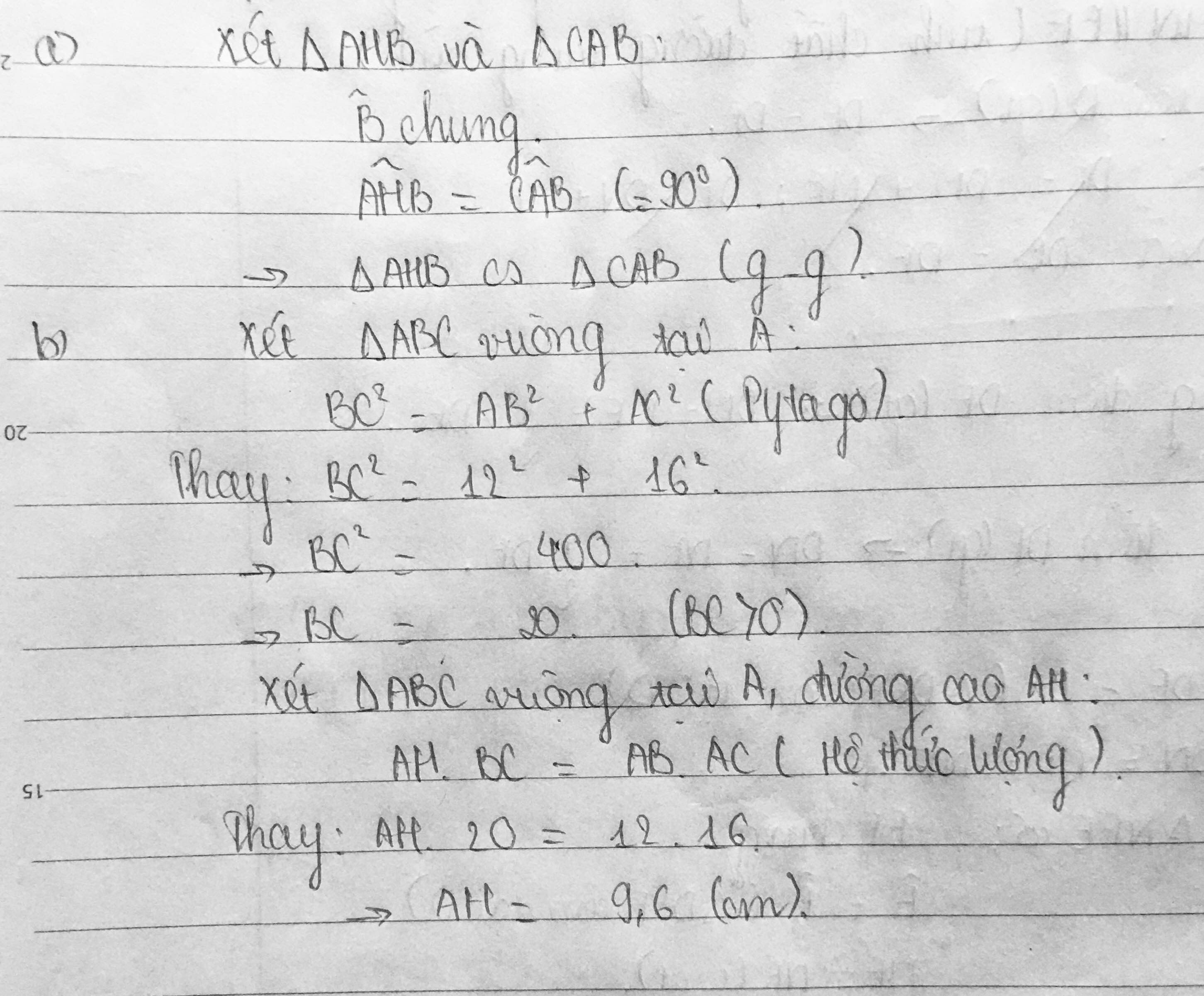Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔDAH vuông tại D và ΔHAC vuông tại H có
\(\widehat{DAH}\) chung
Do đó: ΔDAH\(\sim\)ΔHAC(g-g)

b) Chứng minh tam giác BEC đồng dạng tam giác ADC
Xét \(\Delta CAB\)và \(\Delta CDE\) có:
^CAB = ^CDE (=1v)
^C chung
=> \(\Delta CAB\)~\(\Delta CDE\)
=> \(\frac{CB}{CE}=\frac{CA}{CD}\) (1)
Xét \(\Delta CAD\)và \(\Delta CBE\)có:
\(\frac{CB}{CE}=\frac{CA}{CD}\)( từ (1))
và \(\widehat{C}\)chung
=> \(\Delta CAD\)~ \(\Delta CBE\)
c) Chứng tam giác ABE vuông cân.
+) Ta có: AB \(\perp\)AC (\(\Delta\)ABC vuông )
mà E \(\in\)AC
=> AB \(\perp\)AE => \(\Delta\)ABE vuông
+) Theo (a) => ^DAC = ^EBC
Gọi N là giao điểm của AD và BE
Xét \(\Delta\)DNB và \(\Delta\)ENA có:
^ENA = ^DNB ( đối đỉnh)
^NBD = ^NAE ( vì ^DAC = ^EBC )
=> \(\Delta\)DNB ~ \(\Delta\)ENA
=> ^NDB = ^NEA
Xét \(\Delta\)ABE và \(\Delta\)HAD có:
^AEB = ^HDA ( vì ^NDB = ^NEA ) (1)
^^BAE = ^AHD ( =1v)
=> \(\Delta\)ABE ~ \(\Delta\)HAD
=> ^HAD = ^ ABE (20
mà \(\Delta\)AHD có: AH=HD => \(\Delta\)AHD cân => ^HAD =^ HDA (3)
Từ (1) ; (2) ; (3) => ^ABE =^BEA =>\(\Delta\)ABE cân
Vậy \(\Delta\) ABE vuông cân tại A
d) Ta có: M là trung điểm BE => AM là đường trung tuyến \(\Delta\)ABE mà \(\Delta\)ABE vuông cân tại A
=> AM là đường phân giác ^A của \(\Delta\)ABE
=> AG là đường phân giác ^A của \(\Delta\)ABC
Theo tính chất đường phân giác ta có: \(\frac{GB}{GC}=\frac{AB}{AC}\)
Mà \(\Delta\)ABH ~\(\Delta\)CAH ( dễ tự chứng minh)
=> \(\frac{AB}{CA}=\frac{AH}{CH}\)
=> \(\frac{GB}{GC}=\frac{AH}{CH}\Rightarrow\frac{GB}{AH}=\frac{GC}{CH}=\frac{GB+GC}{AH+CH}=\frac{BC}{AH+CH}\)( tính chất dãy tỉ số bằng nhau)
=> \(\frac{GC}{BC}=\frac{AH}{AH+CH}=\frac{DH}{AH+CH}\)( vì AH=DH)
(tớ mới giải được câu a)
Xét tam giác AHB và CHA => AH/CH = HB/AH mà AH=HD => tỉ số đồng dạng

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE