Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
FG=FD
G,F,D thẳng hàng
Do đó: F là trung điểm của GD
Xét tứ giác ADCG có
F là trung điểm chung của AC và GD
=>ADCG là hình bình hành
Hình bình hành ADCG có AC\(\perp\)GD
nên ADCG là hình thoi

a: Sửa đề; DA=EF
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nen AEDF là hình chữ nhật
=>DA=EF
b: Xét tứ giác AFEH có
AF//HE
AF=HE
Do đó: AFEH là hình bình hành
XétΔABC có
Dlà trung điểm của BC
DE//AC
Do đó E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó:F là trung điểm của AC
Xét tứ giác AHBD có
E là trung điểm chung của AB và HD
AB vuông góc với HD
Do đó: AHBD là hình thoi
=>AB là phân giác của góc HAD(1)
c: Xét tứ giác ADCI có
F là trung điểm chung của AC và DI
DA=DC
Do đó: ADCI là hình thoi
=>AC là phân giác của góc DAI(2)
Từ (1), (2) suy ra góc IAH=2*90=180 độ
=>I,A,H thẳng hàng
mà AI=AH
nên A là trung điểm của IH

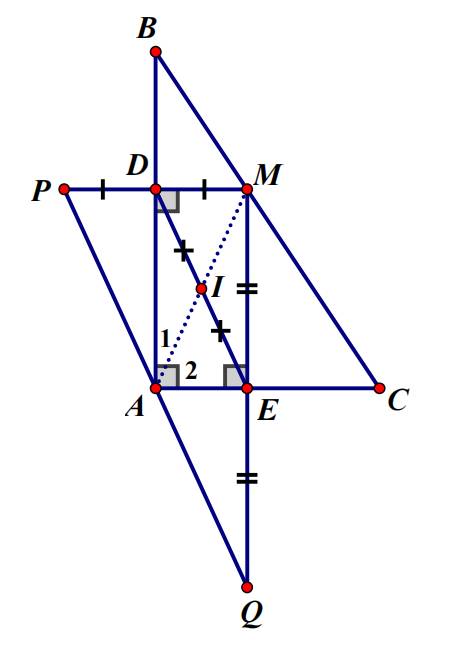
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ

a)Xét tứ giác AMDN có: góc AMD=900
góc MAN=900
góc DNA=900
=> Tứ giác AMDN là hình chữ nhật(dhnb hcn)
b)Xét tam giác ABC vuông tại A có:D là trung điểm của BC
=>AD là đường trung tuyến ứng với cạnh huyền BC
=>AD=BD=CD=BC/2
=> tg ACD cân tại D
Xét tg ACD cân tại D có: DN là đường cao
=>DN là đường trung tuyến của tam giác ADC
=>N là trung điểm của AC
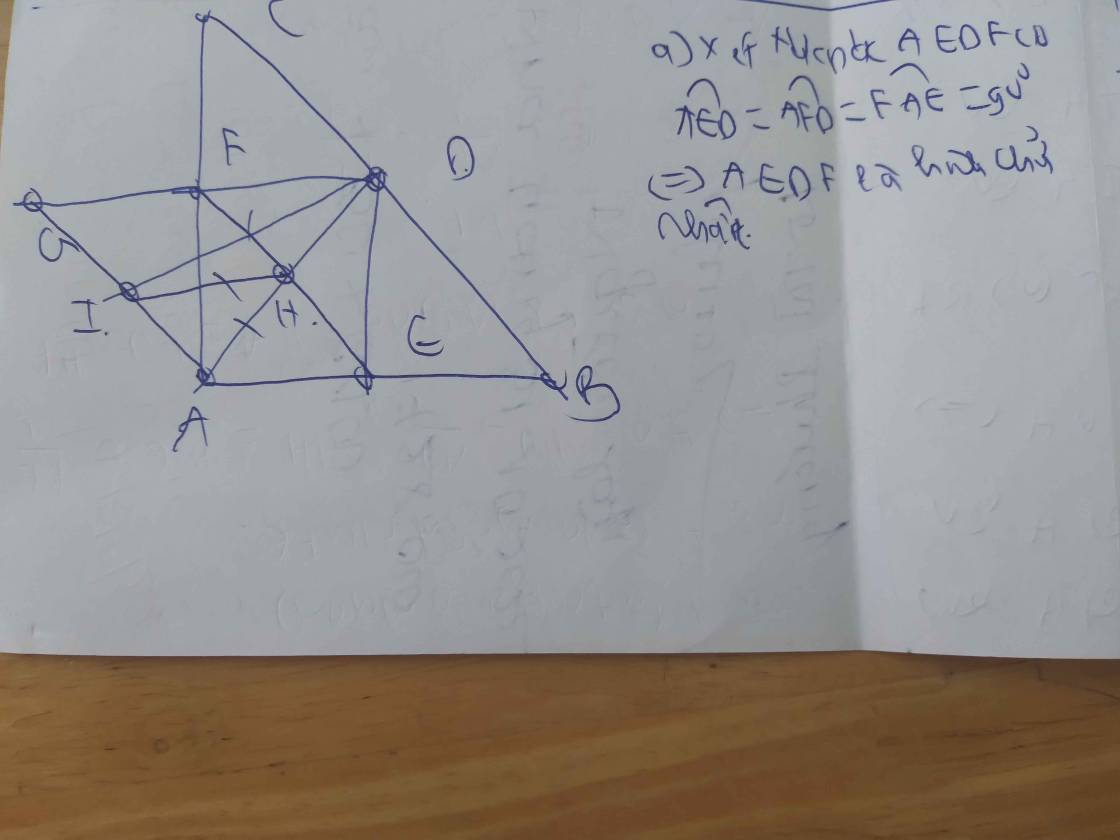



a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó; E là trung điểm của AB
Xét ΔBAC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
Xét tứ giác ADBM có
E là trung điểm chung của AB và DM
=>ADBM là hình bình hành
c: Xét tứ giác ADCN có
F là trung điểm chung của AC và DN
=>ADCN là hình bình hành
=>AN//CD và AN=CD
Ta có: ADBM là hình bình hành
=>AM//BD và AM=BD
Ta có: AN//CD
AM//BD
mà B,D,C thẳng hàng
nên AN//BC và AM//BC
mà AN,AM có điểm chung là A
nên N,A,M thẳng hàng
Ta có: AM=BD
AN=CD
mà BD=DC
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN
cảm ơn bạn