Giúp mình với, mình cảm ơn!😢

a, Xét tam giác HBA vuông tại H có:

AB²=AH²+BH²(định lí py ta go)

hay 100=AH²+36

=> AH²=64

=> AH=8(cm)

b, Xét tam giác ABH và tam giác ACH có:

góc AHB=góc AHC =90 độ

AB=AC (tam giác ABC cân tại A)

AH chung

=> tam giác ABH = tam giác ACH

c,

Xét tam giác DBH và tam giác ECH có:

BD=CE (gt)

góc DBH= góc ECH (tam giác ABC Cân tại A)

BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)

=> tam giác DBH=tam giác ECH

=> DH=EH( 2 cạnh tương ứng)

=> tam giác HDE cân tại H

d) Vì AB = AC; BD = CE

mà AB - BD = AD

AC - CE = AE

=> AD = AE

Vì ΔHDE cân

=> H ∈ đường trung trực cạnh DE (1)

Xét ΔADHvàΔAEHcó

AD = AE (cmt)

AH (chung)

DH = HE (cmt)

Do đó: ΔADH=ΔAEH(c−c−c)

=> AD = AE ( hai cạnh tương ứng)

=> ΔADE cân tại A

=> A ∈ đường trung trực cạnh DE (2)

(1); (2) => A,H ∈ đường trung trực cạnh DE

=>AH là đường trung trực cạnh DE

CHÚC BẠN HỌC TỐT

lỗi r bn

a: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}\)

mà \(\widehat{ABC}=74^0\)

nên \(\widehat{ACB}=74^0\)

Ta có: ΔABC cân tại A

=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}\)

=>\(\widehat{BAC}=180^0-2\cdot74^0=32^0\)

b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có

AB=AC

\(\widehat{BAH}\) chung

Do đó: ΔAHB=ΔAKC

=>AH=AK

=>ΔAHK cân tại A

c: Ta có: ΔAHB vuông tại H

=>\(AH^2+BH^2=AB^2\)

=>\(AH^2=10^2-6^2=64\)

=>\(AH=\sqrt{64}=8\left(cm\right)\)

=>AK=8(cm)

d: Xét ΔAKO vuông tại K và ΔAHO vuông tại H có

AO chung

AH=AK

Do đó: ΔAKO=ΔAHO

=>\(\widehat{KAO}=\widehat{HAO}\)

=>\(\widehat{BAO}=\widehat{CAO}\)

=>AO là phân giác của góc BAC

Diện tích tam giác ABC là:

     6.8:2=24 (cm²)

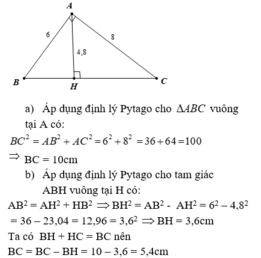
Áp dụng định lí Py-ta-go cho tam giác ABC, ta có:

AB²+AC²=BC²

=>6²+8²=BC²=>36+64=BC²=>BC=10 (cm)

Đường cao AH dài là:

     24.2:10=4,8 (cm)

Áp dụng định lí Py-ta-go cho tam giác ABH, ta có:

AH²+BH²=AB²

=>4,8²+BH²=36

=>23,04+BH²=36

=>BH²=12,96=>BH=3,6 (cm)

Độ dài CH là:

     10-3,6=6,4 (cm)

           Đáp số: AH: 4,8 cm; BH: 3,6 cm; CH: 6,4 cm; BC: 10 cm

\(\text{Áp dụng định lý Pytago ta có:}\)

\(BC^2=AB^2+AC^2\)

\(\Rightarrow BC^2=6^2+8^2\)

\(\Rightarrow BC^2=100\)

\(\Rightarrow BC=10\left(\text{Vì BC}>0\right)\)

\(S_{\Delta ABC}\text{ là}:\)

\(\frac{6.8}{2}=24\)

\(\text{Vì AH là đường cao hạ từ đỉnh A và BC là đáy tương ứng với đường cao AH nên}\)

\(S_{\Delta ABC}=\frac{BC.AH}{2}=\frac{10.AH}{2}=24\)

\(\Rightarrow AH=24:5=4,8\)

\(\text{Áp dụng định lý Pytago ta có:}\)

\(AB^2=AH^2+BH^2\)

\(\Rightarrow6^2=4,8^2+BH^2\)

\(BH^2=12.96\)

\(BH=3,6\)

\(\text{CH thì tính tương tự như BH nha}\)

a) Áp dụng ĐL Pytago ta có: \(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)

b) Xét \(\Delta ABH\) và \(\Delta ADH\) có: 

\(AH\) chung

\(\widehat{AHB}=\widehat{AHD}=90^0\)

\(BH=DH\) (gt)

\(\Rightarrow\Delta ABH=\Delta ADH\left(c.g.c\right)\)

c) Do \(\Delta ABH=\Delta ADH\Rightarrow\widehat{B}=\widehat{ADH}\) mà \(\widehat{ADH}=\widehat{EDC}\) (đối đỉnh)

\(\Rightarrow\widehat{EDC}=\widehat{B}\)

Lại có \(BA//DK\) (do cùng vuông góc \(AC\)) \(\Rightarrow\widehat{KDC}=\widehat{B}\) (đồng vị)

Xét \(\Delta DKC\) và \(\Delta DEC\) có:

\(\widehat{DKC}=\widehat{DEC}=90^0\)

\(CD\) chung

\(\widehat{KDC}=\widehat{EDC}=\widehat{B}\)

\(\Rightarrow\Delta DKC=\Delta DEC\) (ch - gn) \(\Rightarrow DE=DK\)

d) Xét tam giác \(AMC\) có: \(\left\{{}\begin{matrix}MK\perp AC\\AE\perp MC\\MK\cap AE=D\end{matrix}\right.\)

\(\Rightarrow D\) là trực tâm \(\Rightarrow MD\perp AC\) mà \(DK\perp AC\Rightarrow MD\equiv MK\)

\(\Rightarrow MK\perp AC\Rightarrow MK//AB\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>góc BAH=góc CAH

=>AH là phân giác của góc BAC

c: BH=CH=3cm

AH=căn 5^2-3^2=4cm

Áp dụng định lí Pytago tam giác ABC vuông tại A

\(AC=\sqrt{BC^2-AB^2}=12cm\)

Ta có : \(S_{ABC}=\dfrac{1}{2}AB.AC;S_{ABC}=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{60}{13}cm\)

Theo định lí Pytago tam giác ABH vuông tại H

\(BH=\sqrt{AB^2-AH^2}=\dfrac{25}{13}cm\)

-> CH = BC - BH = \(13-\dfrac{25}{13}=\dfrac{154}{13}\)cm