Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
=>AD=ME
b: Xét tứ giác FDGE có
GE//FD
GE=FD
=>FDGE là hình bình hành
=>FG cắt DE tại trung điểm của mỗi đường(1)
ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AM,DE,FG đồng quy
c: góc AHM=góc AEM=góc ADM=90 độ
=>A,D,H,M,E cùng thuộc đường tròn đường kính AM
=>A,D,H,M,E cùng thuộc đường tròn đường kính DE
=>góc DHE=90 độ

a)Xét tứ giác AFDE có :góc AED = 90°(gt)góc EAF = 90 °(gt)góc AFD =90 °(gt)=> Tứ giác AFDE là hình chữ nhật ( dhnb)(đcpcm)
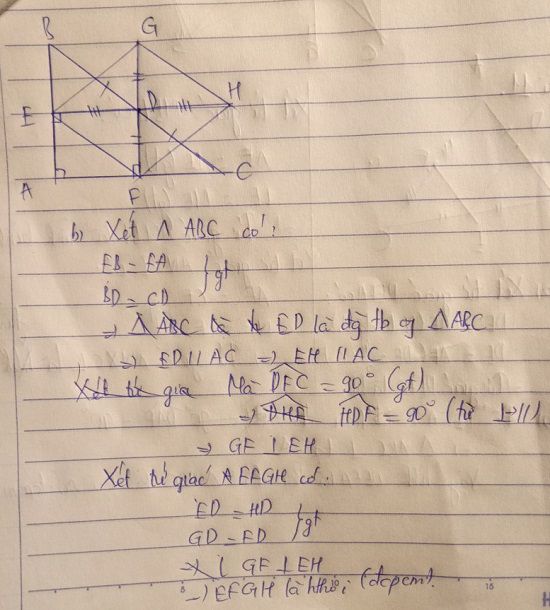


a) Tứ giác \(AMDN\) có \(\widehat{A}=\widehat{M}=\widehat{N}=90^0\)
nên \(AMDN\) là hình chữ nhật
b) MK SỬA LẠI ĐỀ NHA: CM AEBD LÀ HÌNH THOI
\(\Delta ABC\)có \(DB=DC;\)\(DM\)// \(AC\)( cùng \(\perp AB\))
\(\Rightarrow\)\(MA=MB\)
Tứ giác \(AEBD\)có \(MA=MB;\)\(ME=MD\)
nên \(AEBD\)là hình bình hành
mà \(AB\perp ED\)
nên \(AEBD\)là hình thoi