Bài giải

a) Xét tam giác ABH và CAH có:

  \(\widehat{AHB}=\widehat{CHA}\left(=90^o\right)\)

\(\widehat{BAH}=\widehat{ACH}\left(=90^o-\widehat{ABC}\right)\)
\(\Rightarrow\Delta ABH\infty\Delta CAH\left(g.g\right)\)

 \(\Delta ABH\infty\Delta CAH\left(g.g\right)\) (câu a)  \(\Rightarrow\dfrac{AB}{AC}=\dfrac{BH}{AH}=\dfrac{BH\text{ : }2}{AH\text{ : 2}}=\dfrac{BP}{AQ}\)

Xét \(\Delta ABP \text{và }\Delta CAQ\) có: $\frac{BP}{AQ}=\frac{AB}{AC}$

                                        \(\widehat{CAH}=\widehat{ABH}\left(=90^o-\widehat{BAH}\right)\)

\(\Rightarrow\Delta ABP\infty\Delta CAQ\left(c.g.c\right)\)

b, Ta có: PQ là đg trung bình của\(\Delta ABH\Rightarrow\text{ }PQ\text{ // }AB\text{ }\Rightarrow\text{ }PQ\perp AC\)  

Mà AH$\perp$PC  => Q là trực tâm của \(\Delta APC\)

\(\Rightarrow\text{ }AP\perp CQ\)

2 tam giác đồng dạng

Bạn tự vẽ hình nha!

a, Xét Tg ABH và CAH có:

  AHB=CHA  (=90)

  BAH=ACH (=90-ABC)

=>  ABH đồng dạng CAH (g.g)

b, Tg ABH đồng dạng CAH (câu a)  => \(\frac{AB}{AC}=\frac{BH}{AH}=\frac{BH:2}{AH:2}=\frac{BP}{AQ}\)

Xét Tg ABP và CAQ có: \(\frac{BP}{AQ}=\frac{AB}{AC}\)

                                        CAH=ABH  (=90-BAH)

=> Tg ABP đồng dạng CAQ (c.g.c)

c, Ta có: PQ là đg trung bình của Tg ABH  => PQ//AB => PQ \(\perp\)AC

Mà AH\(\perp\)PC  => Q là trực tâm của Tg APC

=> AP \(\perp\)CQ

bây giờ bạn có cách làm bài này chưa, chỉ tôi zs

hình tự kẻ nha (((=

a)

+/    xét tam giác ABH và tam giác CAH có :

                góc AHB = góc AHC = 90 độ

                góc ABH = góc CAH ( cùng phụ góc BAH)

do đó tam giác ABH đồng dạng với tam giác CAH (trường hợp góc - góc ) 

=)) AB/AC=BH/AH  (1)

ta có BH/AH=2PB/2AQ =PB/AQ (2)

(1),(2) =)) AB/AC=PB/AQ (3)

+/   xét tam giác ABP và tam giác CAQ có:

                       góc ABP = góc CAQ ( cùng phụ góc BAH )

                       PB/AQ=AB/AC  ( do (3) )

 dó đó tam giác ABP đồng dạng với tam giác CAQ      

=))    (ĐPCM)

tạm thời được câu a)   câu b) chưa nghĩ ra 

nghĩ ra mình làm tiếp cho

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Ta có: ΔHAC\(\sim\)ΔABC(cmt)

nên \(\dfrac{AH}{AB}=\dfrac{AC}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)

\(\Leftrightarrow\dfrac{AH}{6}=\dfrac{8}{10}=\dfrac{4}{5}\)

hay AH=4,8(cm)

Vậy: AH=4,8cm

a) Xét ΔHAC vuông tại H và ΔABC vuông tại A có 

\(\widehat{ACH}\) chung

Do đó: ΔHAC\(\sim\)ΔABC(g-g)

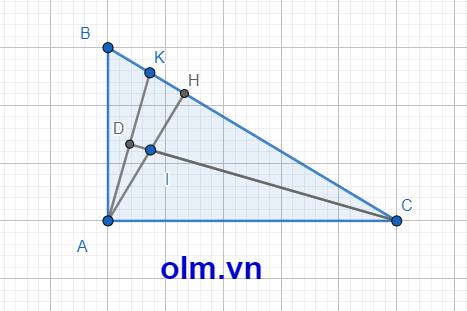
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\)  =  \(\widehat{A}\) = 90⁰; \(\widehat{B}\) chung

⇒  \(\Delta\) HBA  \(\sim\)  \(\Delta\) ABC (g-g)

Tương tự ta có:   \(\Delta\) HAC  \(\sim\)  \(\Delta\) ABC (g-g-g)

    ⇒ \(\Delta\) HBA  \(\sim\)   \(\Delta\) HAC ( t/c hai tam giác đồng dạng)

   ⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)

Mặt khác: KI là đường trung bình của tam giác ABH nên:

        \(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒  \(\dfrac{HK}{HI}\) =   \(\dfrac{HB}{HA}\)

⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\)  = 90⁰

⇒ \(\Delta\)  AHK \(\sim\) \(\Delta\) CHI ( c-g-c)

b, Kéo dài CI cắt AK tại D ta có:

vì  \(\Delta\)  AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)

Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)

                                           \(\widehat{K}\) chung

   ⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)

  ⇒ \(\widehat{H}\) = \(\widehat{D}\)= 90⁰ ⇒ AK \(\perp\) CI tại D ( đpcm)