Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác AHB và tam giác DHB có:
góc H = 90 độ
HB chung
AB=DB (gt)
=> tam gaics AHB = tam giác DHB ( cạnh huyền cạnh góc vuông)
=> AH = HD ( 2 cạnh tương ứng)
b) Chứng min htuowng tự có có:
tam giác AKC = tam giác EKC ( cạnh huyền - cạnh góc vuông)
=> AK = KE ( 2 cạnh tương ứng)
*) Xét tám giác ADE có:
AH = HD ( cmt)
AK = KE ( cmt)
=> HK alf đường trung bình của hình thang
=> HK//DE hay nói cách khác
HK // DB

a) Vì \(\frac{CD}{AC}=\frac{1,5}{3}=\frac{1}{2}\); \(\frac{CE}{BC}=\frac{2,5}{5}=\frac{1}{2}\)
Nên \(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Xét ΔCDE và ΔCAB có
\(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Góc DCE=ACB(đối đỉnh)
Vậy hai tam giác đồng dạng với nhau
=> Góc CDE=CAB=90 độ
Vậy ΔCDE là tam giác vuông.
Áp dụng định lí Pi-ta-go vào ΔCDE ta có:
\(CE^2=DC^2+DE^2\Rightarrow DE^2=CE^2-CD^2=2,5^2-1,5^2=4\)
=> \(DE=\sqrt{4}=2cm\).
b) Vì ΔCDE đồng dạng với ΔCAB nên
\(\frac{CD}{AC}=\frac{DE}{AB}\Rightarrow AB=\frac{AC.DE}{CD}=\frac{3.2}{1,5}=4\left(cm\right)\)
ΔABC vuông tại A, đường cao AH, theo hệ thức lượng, ta có:
- \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{4.3}{5}=2,4\left(cm\right)\)
- \(AC^2=CH.BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{3^2}{5}=\frac{9}{5}=1,8\left(cm\right)\)
\(CH=BC-CH=5-1,8=3,2\left(cm\right)\)

bạn vô đây coi bài nào thích hớp thì xem Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kể từ B đến AD, K là chân đường vuông góc kẻ từ C đến AE a) Chứng minh rằng HK song song với DE b) Tính HK, biết chu vi tam giác ABC bằng 10 cm Bài 2 Cho tam giác ABC, đường trung tuyến AM. Trên tia đối của tia AM lấy điểm N sao cho AN = AM. Gọi K là giao điểm của CA và NB. Chứng minh NK = 1/2 KB... Xem thêm - Tìm với Google

Cậu tự vẽ hình nhé
a, kẻ MK vuông BC, NG vuông BC
Tam g ABC cân => g ABC= g ACB
Lại có g ACB = g GCN (dd)
=> g GCN = g ABC=g MBK
Xét tg MBK và tg NCG
g MKB= g NGC =90°
g MBK = g NCG (cmt)
MB= CN(gt)
=> tg MBK= tg NCG ( ch-gn)
=> MK=NG (2 cạnh tương ứng)
Vì MK vuông BC, NG vuông BC => NG// MK
=> g GNM = g KMN ( so le trong )
Xét tg MKD VÀ TG NGD
g MKD = g DGN = 90°
g KMD = gDNG ( cmt)
Mk= GN (cmt)
=> tg MKD = tg NGD (_cgv-gn)
=> MD= ND (2 ctu)
=> D là td MN ( dpcm)
Xét tam giác cân ABC , AH là đường cao => AH là trung trực
Lại có E thuộc AH => EC= EB
Xét tg ABE và tg ACE
AB=AC (tg ABC cân)
BE= EC (cmt)
AE cạnh chung
=> tg ABE = tg ACE (ccc)
=> g ABE = g ACE ( 2 góc tương ứng)(1)
Lại có DE là trung trực MN => ME = NE
Xét tg MBE và tg NCE
MB = NC ( gt)
ME = NE (cmt)
BE = CE (cmt)
=> tg MBE = tg NCE (ccc)
=> g ECN = g EBM (2 góc t u ) (2)
Từ 1), 2) => g ECA = g ECN
Lại có 2 góc này bù nhau
=>g ACE= 90°= g ABE
Xét tg ABE vuông
+ theo đl pytago:
=> AE = √( ab2+bE2)= √( 62+4,52)= 7,5 (cmcm)
+ BH là đcao, theo hệ thức lượng trong tg vuông
=>+ AB2= AH.AE => AH= 62:7,5=4,8 (cmcm)
+ 1/(BH2)= 1/(AB2)+1/(BE2) => BH = √(1:( (1/62)+(1/4,52))= 3,6(ccmcm)
=> BC= 3,6.2= 7,2 (cm)
=> dt tg ABC có đcao AH là 7,2.4,8.1/2= 28,08(cm2)
Vậy S tg ABC = 28,08 cm2

GIẢI: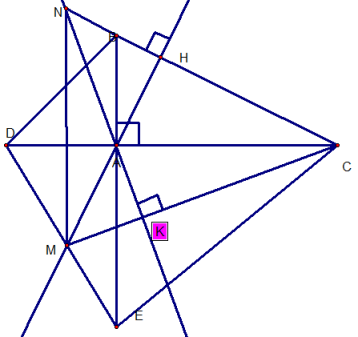
a) Xét Δ ABC và Δ AED, ta có :
(đối đỉnh)
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
(Δ ABC vuông tại A)
=> AD AE
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : ở vị trí so le trong
=> BD // CE
b) Xét Δ MNC, ta có :
NK MC = > NK là đường cao thứ 1.
MH NC = > MH là đường cao thứ 2.
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN AC tại I.
mà : AB AC
=> MN // AB.
c) Xét Δ AMC, ta có :
(đối đỉnh)
(Δ ABC = Δ AED)
=> (cùng phụ góc ABC)
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
(MN
AC tại I)
IM cạnh chung.
mặt khác : (so le trong)
(đồng vị)
mà : (cmt)
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.


grade 7??