Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (A;AH) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;AH)
b: Xét (A) có
BH,BD là các tiếp tuyến
Do đó: BH=BD và AB là phân giác của góc HAD
Xét (A) có
CE,CH là các tiếp tuyến
Do đó: CE=CH và AC là phân giác của góc HAE
c: BD+CE
=BH+CH
=BC
d: AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
AC là phân giác của góc HAE
=>\(\widehat{HAE}=2\cdot\widehat{HAC}\)
Ta có: \(\widehat{HAD}+\widehat{HAE}=\widehat{EAD}\)
=>\(\widehat{EAD}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{EAD}=2\cdot\widehat{BAC}=180^0\)
=>E,A,D thẳng hàng

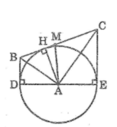
Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có:
AD ⊥ DB; AE ⊥ CE
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: MA // BD ⇒ MA ⊥ DE
Trong tam giác vuông ABC ta có : MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC.
b: Xét (A) có
CH,CE là tiếp tuyến
=>CH=CE
Xét (A) có
BH,BD là tiếp tuyến
=>BH=BD
BC=BH+CH
=>BC=BD+CE
c: Xét tứ giác AHCE có
góc AHC+góc AEC=180 độ
=>AHCE nội tiếp