cho \(\Delta ABCD\)

a: Xét tứ giác ADEF ccó

gócc ADE=góc AFE=góc FAD=90 độ

nên ADEF là hình chữ nhật

b: Xét tứ giác AECK có

Dlà trung điểm chung của AC và EK

EA=EC

Do đó: AECK là hình thoi

c: ΔEMA vuông tại M

mà MO là trung tuyến

nên MO=EA/2=DF/2

Xét ΔMDF có

MO là trung tuyến

MO=DF/2

Do đó: ΔMDF vuông tại M

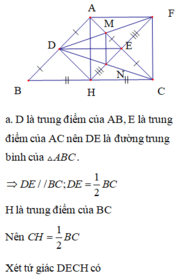
a) Xét ∆ABC có : 

D là trung điểm AB 

E là trung điểm BC 

=> DE là đường trung bình ∆ABC 

=> DE//AC , DE = \(\frac{1}{2}AC\)= \(\frac{16}{2}=8\)cm

Xét ∆ABC có : 

E là trung điểm BC 

F là trung điểm AC 

=> FE là đường trung bình ∆ABC 

=> FE//AB , FE = \(\frac{1}{2}AB=6cM\)

Xét tứ giác AFED có : 

AD//EF ( AB//FE , D\(\in\)AB )

DE//FA ( DE//AC , F \(\in\)AC )

=> AFED là hình bình hành 

Mà BAC = 90° 

=> AFED là hình chữ nhật 

=> DEF= EFA = FAD = ADE = 90° 

Vì F là trung điểm AC 

=> FA = FC = 8cm

Áp dụng định lý Py - ta -go vào ∆AEF ta có : 

AE² = FE² + AF² 

=> AE = 10cm

b) Xét ∆ABC ta có : 

D là trung điểm AB 

F là trung điểm AC 

=> DF là đường trung bình ∆ABC 

=> DF//BC  

Xét tứ giác BEFD ta có : 

BE//DF ( BC//DF , E \(\in\)BC )

BD//FE ( AB//FE , D\(\in\)AB )

=> BEFD là hình bình hành 

c) Chứng minh trên 

a: Xét tứ giác ADEF có

\(\widehat{ADE}=\widehat{AFE}=\widehat{DAF}=90^0\)

=>ADEF là hình chữ nhật

b: Xét ΔABC có

E là trung điểm của CB

ED//AB

Do đó: D là trung điểm của AC

Xét tứ giác AECK có

D là trung điểm chung của AC và EK

=>AECK là hình bình hành

Hình bình hành AECK có AC\(\perp\)EK

nên AECK là hình thoi

c: Xét ΔABC có

E,D lần lượt là trung điểm của CB,CA

=>ED là đường trung bình của ΔABC

=>\(ED=\dfrac{AB}{2}\)

mà \(ED=\dfrac{EK}{2}\)

nên EK=AB

Ta có: ED//AB

D\(\in\)EK

Do đó: EK//AB

Ta có: ADEF là hình chữ nhật

=>AE cắt DF tại trung điểm của mỗi đường

=>O là trung điểm chung của AE và DF

Xét tứ giác ABEK có

KE//AB

KE=AB

Do đó: ABEK là hình bình hành

=>AE cắt BK tại trung điểm của mỗi đường và AE=BK

mà O là trung điểm của AE

nên O là trung điểm của BK

=>B,O,K thẳng hàng

ΔEMA vuông tại M

mà MO là đường trung tuyến

nên \(MO=\dfrac{AE}{2}\)

mà AE=DF

nên \(MO=\dfrac{DF}{2}\)

Xét ΔDMF có

MO là đường trung tuyến

MO=DF/2

Do đó: ΔDMF vuông tại M

=>\(\widehat{DMF}=90^0\)

a) Xét tứ giác ADEF có : góc A = 90 độ ( tam giác ABC vuông tại A)

                                      góc EFA = 90 độ ( EF vuông góc với AB tại F)

                                      góc EDA = 90 ( ED vuông góc với AC tại D)

suy ra : ADEF là hcn

b) Xét tam giác ABC có : BE = EC ( E là trung điểm của BC )

                                        ED song song với AB ( EFAD là hcn )

suy ra : AD = DC

Xét tứ giác AECK có : ED = DK ( E đối xứng với K qua D )

                                    AD = DC (cmt)

suy ra : tứ giác AECK là hình bình hành 

mà ED vuông góc với AC 

suy ra : hbh AECK là hình thoi

Bài 1:

a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)

\(\Rightarrow ME\)là đường trung bình tam giác ABC

\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)

Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)

\(\Rightarrow PE\)là đường trung bình của tam giác ADC

\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)

mà \(AD=BC\left(gt\right)\left(3\right)\)

Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)

CMTT: \(PE=FP,FM=ME\)

\(\Rightarrow ME=EP=PF=FM\)

Xét tứ giác MEPF có:

\(ME=EP=PF=FM\left(cmt\right)\)

\(\Rightarrow MEPF\)là hình thoi ( dhnb)

 b) Vì \(MEPF\)là hình thoi (cmt)

\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc)  (4)

Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)

\(\Rightarrow MQ\)là đường trung bình của tam giác ADB

\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)

Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)

\(\Rightarrow NP\)là đường trung bình của tam giác BDC

\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)

Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)

Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)

\(\Rightarrow MQPN\)là hình bình hành (dhnb)

\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)

Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm 

c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)

\(\Rightarrow QF\)là đường trung bình của tam giác ADB

\(\Rightarrow QF//AB\left(8\right)\)

CMTT: \(FN//CD\)và \(EN//AB\)

Mà Q,F,E,N thẳng hàng 

\(\Rightarrow AB//CD\)

Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện  \(AB//CD\)

Tối về mình làm nốt  nhé giờ mình có việc 

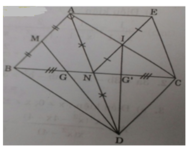
a) Ta có: NB = NC (gt); ND = NA (gt)

⇒ Tứ giác ABDC là hình bình hành

có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.

b) Ta có: AI = IC (gt); NI = IE (gt)

⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).

mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.

Vậy tứ giác AECN là hình thoi.

c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.

Tương tự G’ là trọng tâm của hai tam giác ACD

⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’

d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)

Lại có: BG = GG’ = CG’ (tính chất trọng tâm)

⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD

(chung đường cao kẻ từ D và đáy bằng nhau)

Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))

⇒SDGG' = 24/3 = 8(cm2)

SDGB là S tam giác DGB pk ạ ?