Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
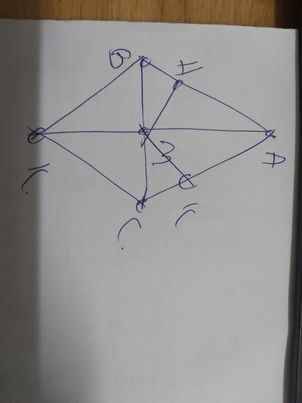
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M

a: Xét ΔABM và ΔACM có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABDC có
M là trung điểm của BC
M la trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a/ Xét t/g BMH và t/g CMK có:
BM = CM (gt)
\(\widehat{BMH}=\widehat{CMK}\) (đối đỉnh)
MH = MK (gt)
=> t/g BMH = t/g CMK (c.g.c)(đpcm)
b/ Vì t/g BMH = t/g CMK (ý a)
=> \(\widehat{MBH}=\widehat{KCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên:
=> CK // AB (đpcm)
c/ Xét t/g ABM và t/g DCM có:
MA = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
BM = CM (gt)
=> t/g ABM = t/g DCM (c.g.c)
=> \(\widehat{BAM}=\widehat{CDM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên:
=> AB // DC
Ta lại có: CK // AB (ý b)
mà DC // AB (cmt)
=> CK trùng DC
=> 3 điểm D, K, C thẳng hàng(đpcm)

a.
Xét tam giác AHM và tam giác DCM có:
AM = DM (gt)
AMH = DMC (2 góc đối đỉnh)
MH = MC (M là trung điểm của HC)
=> Tam giác AHM = Tam giác DCM (c.g.c)
b.
AHM = DCM (tam giác AHM = tam giác DCM)
mà AHM = 90độ
=> DCM = 90độ
Tam giác ABC vuông tại A có:
ABC + ACB = 90độ
60độ + ACB = 90độ
ACB = 90 - 60
ACB = 30độ
ACD = ACB + DCM = 30 + 90 = 120độ
a) C/M tam giác AHM= tam giác DCM
Xét tam giác AHM và tam giác DCM, ta có:
MA=MD (gt)
góc AMH= góc DMC (đđ)
MH=MC (gt)
Vậy tam giác AHM= tam giác DCM (c-g-c)
b) Tính góc ACD
Ta có tam giác ABC vuông tại A có góc B=600 nên góc ACB=300
Lại có góc MCD= góc AHM = 900 (hai tam giác bằng nhau)
Vậy góc ACD= 300 + 900 = 1200
c) C/M AK=CD
Trong tam giác AHK, ta có AN đường cao đồng thời là trung tuyến ( AN vuông góc HK và NH=NK)
Nên tam giác AHK cân tại A
Suy ra AK=AH
Mà AH=CD (hai tam giác bằng nhau)
Vậy AK=CD
d) C/M K, H, D thẳng hàng
Ta có tam giác AHC= tam giác DCH ( c-g-c)
Nên góc ACH= góc DHC
Mà hai góc này ở vị trí so le trong
Suy ra AC//HD
Lại có HK//AC ( cùng vuông góc với AB)
Vậy K, H, D thẳng hàng