Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

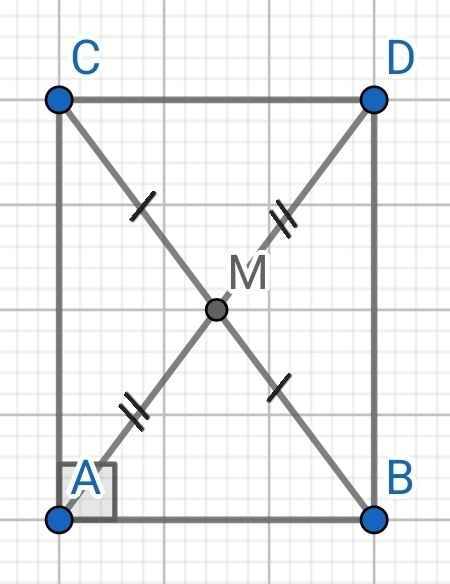
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC

a) Xét tam giác CMA và tam giác BMD có :
\(\hept{\begin{cases}MC=MB\\AM=MD\\\widehat{AMC}=\widehat{BMD}\end{cases}\Rightarrow\Delta CMA=\Delta BMD}\)
=> \(\hept{\begin{cases}AC=BD\\\widehat{BDM}=\widehat{ACM}\end{cases}\Rightarrow BD//AC}\)
=> ACBD là hình bình hành
=> \(\hept{\begin{cases}AB=CD\\AB//CD\end{cases}}\)=> đpcm
b) Xét tam giác ABC và tam giác CDA có :
\(\hept{\begin{cases}AB=CD\\\widehat{CAB}=\widehat{ACD}=90^∗\end{cases}\Rightarrow\Delta ABC=\Delta CDA}\)( Lưu ý : Vì không có dấu kí hiệu " độ " nên em dùng tạm dấu *)
Chung AC
=> AD=BC
=> \(AM=\frac{1}{2}.AD=\frac{1}{2}.BC\)=> đpcm
c) Xét tam giác ABC có :
M là trung điểm BC
A là trung điểm CE
Từ 2 điều trên =>AM là đường trung bình => AM//BE ( đpcm )
e) AM //BE => AD // BE
Tam giác CBE có BA vừa là đường cac ,vừa là trung tuyến => tam giác CBE cân ở B
=> \(\hept{\begin{cases}BC=BE\\AD=BC\end{cases}\Rightarrow AD=EB}\)
Mà AD//BE => ABDE là hình bình hành => AB cắt DE ở trung điểm
=> E,O , D thẳng hàng => đpcm

Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

a, Xét △BMA và △CMD
Có: MB = MC (gt)
BMA = CMD (2 góc đối đỉnh)
MA = MD (gt)
=> △BMA = △CMD (c.g.c)
=> MBA = MCD (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AB // CD (dhnb)
Mà AB ⊥ AC (gt)
=> CD ⊥ AC (từ vuông góc đến song song)
Xét △ABC vuông tại A và △CDA vuông tại C
Có: AC là cạnh chung
AB = DC (△BMA = △CMD)
=> △ABC = △CDA (2cgv)
b, △ABC = △CDA (cmt)
=> BC = AD (2 cạnh tương ứng)
=> BC = 2AM
=> AM = BC : 2

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AC=BD
b: Ta có: ABDC là hình chữ nhật
nên \(\widehat{ABD}=90^0\)
c: ta có:ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2

c: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2
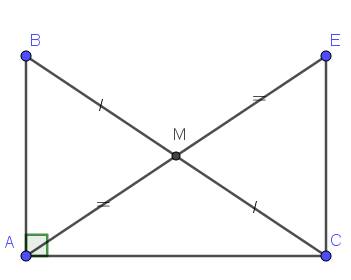
GT: Δ ABC vuông tại A
BM = CM
D ϵ tia đối của tia MA sao cgo MA = MD
KL: AD = BC
\(AM=\frac{1}{2}BC\)
Ta có hình vẽ:
Nối đoạn BD
Xét Δ BMD và Δ CMA có:
BM = CM (gt)
BMD = CMA (đối đỉnh)
MD = MA (gt)
Do đó, Δ BMD = Δ CMA (c.g.c)
=> BD = AC (2 cạnh tương ứng) và BDM = MAC (2 góc tương ứng)
Mà BDM và MAC là 2 góc so le trong nên BD // AC
=> BAC + ABD = 180o (trong cùng phía)
=> 90o + ABD = 180o
=> ABD = 180o - 90o = 90o = BAC
Xét Δ ABD và Δ BAC có:
BD = AC (cmt)
ABD = BAC = 90o
AB là cạnh chung
Do đó, Δ ABD = Δ BAC (c.g.c)
=> AD = BC (2 cạnh tương ứng) (1)
Mà AM = MD = \(\frac{1}{2}AD\) (2)
Từ (1) và (2) => \(AM=\frac{1}{2}BC\left(đpcm\right)\)
Tứ giác ABCD có M là trung điểm của BC và AD
=> Tứ giác ABCD là hình bình hành có góc A=900
=> Hình bình hành ABCD là hình chữ nhật.
=> AD=BC
=> AM=DM=BM=CM
Mà BM + MC = BC
=> AM= 1/2 BC