Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt BC = a, CA = b, AB = c.
Do tam giác ABC vuông tại A nên: \(a^2=b^2+c^2\) (định lý Pytago).
Ta tính được: \(m=\dfrac{a+c-b}{2};n=\dfrac{c+b-a}{2}\).
Từ đó: \(mn=\dfrac{\left(a+c-b\right)\left(c+b-a\right)}{4}=\dfrac{c^2-\left(a-b\right)^2}{4}=\dfrac{\left(a^2+b^2\right)-\left(a-b\right)^2}{4}=\dfrac{ab}{2}=S_{ABC}\).
Vậy...

a: Xét ΔCIB có
CK,BA là đường cao
CK cắt BA tại H
=>H là trực tâm của ΔCIB
=>IH vuông góc BC

a: Xét ΔCIB có
CK,BA là đường cao
CK cắt BA tại H
=>H là trực tâm của ΔCIB
=>IH vuông góc BC

- Trường hợp tam giác vuông:
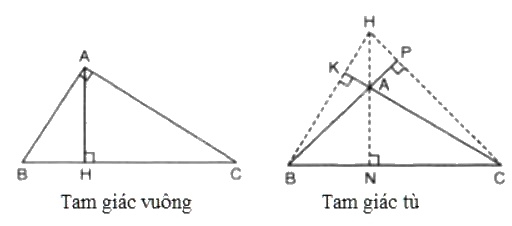
+) Xét tam giác ABC vuông tại A thì BA ⊥ CA hay A là giao điểm của hai đường vuông góc trong tam giác
⇒⇒ A trực tâm của tam giác.
Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.
+) Trường hợp tam giác tù:
Từ B kẻ đường thẳng BK vuông góc với CA.
Ta có: KA, KC lần lượt là hình chiếu của BA, BC.
Vì BC > BA nên KC > KA hay K phải nằm ngoài đoạn thẳng AC. Do đó ta có đường cao BK như hình vẽ.
Tương tự với đường cao CP.
Gọi H là giao điểm của BK và CP
⇒⇒ H chính là trực tâm của tam giác.
Ta thấy H ở bên ngoài tam giác.
Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác đó.
Cách 2:
+ Xét ΔABC vuông tại A
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
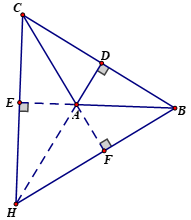
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B, khi đó
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
https://www.google.com/search?sxsrf=ACYBGNShkLL-JlrB5LGT8WMfh0jTHv-mgw:1581944122307&q=-Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+c%C3%A2n+t%E1%BA%A1i+A.+G%E1%BB%8Di+I,+K+theo+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB,+AC.+G%E1%BB%8Di+H,D+th%E1%BB%A9+t%E1%BB%B1+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+I,A+tr%C3%AAn+BK,+M+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+A+tr%C3%AAn+HI.+O+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BM+v%C3%A0+AC+,P+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AB+v%C3%A0+DM+a)+C/m+tam+gi%C3%A1c+DAK+%3D+tam+gi%C3%A1c+HBI+b)+T%C3%ADnh+s%E1%BB%91+g%C3%B3c+ADC+c)C/m+OP+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC&tbm=isch&source=univ&sa=X&ved=2ahUKEwi7rNuL0djnAhUKzTgGHYr8DnMQsAR6BAgDEAE&biw=1137&bih=692

Toán lớp 8 thì mik nghĩ bn vào lazi.vn hoặc hoc.24h.vn để hỏi nha
~ Hok tốt ~
#JH
a)
Xét tam giác ABC ta có
\(AB^2+AC^2=BC^2\)(định lý py ta go)
144 + 256 = BC2
400 = BC2
BC = 20 ( cm )
Xét tam giác ABC có
BD là đường phân giác của tam giác
nên AD/DC = AB/BC = 16/20 = 4/5
có AD + DC = AC = 16
dễ tìm ra AD = 64/9 (cm)
DC = 80/9 (cm)
b) xét 2 tam giác HBA và ABC
có góc ABC chung
2 góc AHB và CAB bằng nhau cùng bằng 90 độ
nên 2 tam giác HAB và ABC đồng dạng với nhau
c)
có 2 tam giác HAB và ABC đồng dạng với nhau
nên \(\frac{S_{HAB}}{S_{ABC}}=\left(\frac{AB}{BC}\right)^2=\left(\frac{12}{20}\right)^2=\frac{9}{25}\)
d)
có E là hình chiếu của của C trên BD
nên \(CE\perp BD\)
suy ra \(\widehat{BEC}=90^0\)
xét 2 tam giác BHK và BEC
có \(\widehat{BHK}=\widehat{BEC}=90^0\)
\(\widehat{CEB}\)chung
nên 2 tam giác BHK và BEC đồng dạng với nhau
suy ra \(\frac{BH}{BE}=\frac{BK}{BC}\Rightarrow BH\cdot BC=BK\cdot BE\)(1)
có 2 tam giác HAB và ABC đồng dạng với nhau
suy ra \(\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\left(2\right)\)
từ (1) và (2) suy ra
\(AB^2=BK\cdot BE\)

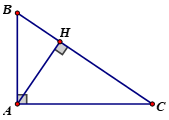
a, Xét tg ABC và tg HBA có:
góc H = góc A (= 90o)
góc B chung
=> Tg ABC đông dạng với tg HBA
Câu b, lm theo cách của mk thì hơi dài dòng bn muốn tham khảo thì mk sẽ lm còn câu c, thì mk phải lm đc câu b đã thì sẽ ra câu c
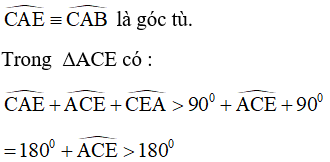
kẻ IE vuông vs AC ; ID vuông vs AB
do Bi là p/g góc ABC
CI là p/g góc ACB
suy ra ID=IK
lại có ID//AE ( cung vuông vs AD)
IE//AD ( cùng vuông vs AE )
suy ra ID=IE=AD=AE=IK
đặt ID=IE=AD=AE=IK=x
xét tam giác BIK= tam giác BID
=) BD=BK=a
tương tự =) CK=CE=b
áp dụng định lí py ta go cho ABC vuông tại A ta có:
AB^2 + AC^2= BC^2
(a+x)^2 + (b+x)^2 = (a+b)^2
ax + bx +x^2 =ab
( phần sau tự lm)