Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔABE=ΔDBE
b: Ta có: ΔABE=ΔDBE
=>BA=BD và EA=ED
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BE là đường trung trực của AD
=>BE\(\perp\)AD
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)(hai góc đối đỉnh)
Do đó: ΔEAF=ΔEDC
=>EF=EC
=>ΔEFC cân tại E

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: ta có: ΔBAE=ΔBDE
nên BA=BD và EA=ED
=>BE là đường trung trực của AD
hay BE\(\perp\)AD

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b, Ta có : góc BAD = góc BED=90 độ (hai góc tương ứng)
=> góc BED là góc V
Ta có ; DA=DE (hai cạnh tương ứng)

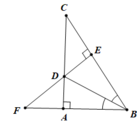
d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc FBE chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔBFC cân tại B
mà BD là phân giác
nên BD vuông góc CF
=>BD//AH
=>AH vuông góc AE

a) Xét ΔABD và ΔEBD có
BD là phân giác => góc ABD = góc EBD
BD chung
Góc BAD = góc BED =90o
=> ΔABD = ΔEBD (ch-gn)
=>AD=ED(2 cạnh tương ứng)
b) xét ΔADF và ΔEDC có
Góc DAF= góc DEC=90o
AD=ED (cmt)
Góc ADF=EDC( đối đỉnh)
=>ΔADF = ΔEDC (gcg)
=> AF=EC(2 cạnh tương ứng)
c) ta có ΔABD = ΔEBD (cmt)
=> AB = EB (2 cạnh tương ứng)
=> ΔBAE cân tại B
=> \(\widehat{BAE}=\widehat{BEA}=\)\(\dfrac{180 - \widehat{B}}{2}\)(1)
ta lại có AF=EC (cmt)
=> AB+AF=BE+EC
=> BF=BC
=> ΔBFC cân tại B
=>\(\widehat{BFC}=\widehat{BCF}=\dfrac{180-\widehat{B}}{2}\)(2)
từ (1) và (2) => \(\widehat{BFC}\)=\(\widehat{BAE}\) mà 2 góc ở vị trí đồng vị
=> AE//FC

a. Hình vẽ (0.5 điểm)
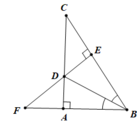
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)
Sửa đề: F là giao điểm của tia BA và tia ED
Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D