Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

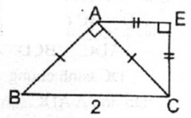
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông

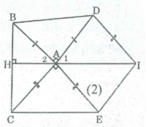
∠ (BAD) + ∠ (BAC) + ∠ (DAE) + ∠ (EAC) = 360 0
Lại có: ∠ (BAD) = 90 0 , ∠ (EAC) = 90 0
Suy ra: ∠ (BAC) + ∠ (DAE) = 180 0 (1)
AE // DI (gt)
⇒ ∠ (ADI) + ∠ (DAE) = 180 0 (2 góc trong cùng phía)
Từ (1) và (2) suy ra: ∠ (BAC) = ∠ (ADI)
Xét ∆ ABC và ∆ DAI có:
AB = AD ( vì tam giác ABD vuông cân).
AC = DI ( = AE)
∠ (BAC) = ∠ (ADI) ( chứng minh trên)
Suy ra: ∆ ABC = ∆ DAI (c.g.c) ⇒ IA = BC