Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\) \(\left\{{}\begin{matrix}AM=MB\\BN=NC\end{matrix}\right.\Rightarrow\) MN là đường trung bình tam giác ABC
\(\Rightarrow MN//AC\Rightarrow MN\perp AB\left(AC\perp AB\right)\)
\(b,MN=\dfrac{1}{2}AC\left(tính.chất.đtb\right)\)
Mà \(AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-12^2}=5\left(cm\right)\left(pytago\right)\)
\(\Rightarrow MN=\dfrac{5}{2}\left(cm\right)\)
\(c,\left\{{}\begin{matrix}AM=MB\\AP=PC\end{matrix}\right.\Rightarrow\) MP là đường trung bình tam giác ABC
\(\Rightarrow MP=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\)
\(\left\{{}\begin{matrix}AP=PC\\BN=NC\end{matrix}\right.\Rightarrow\) NP là đường trung bình tam giác ABC
\(\Rightarrow NP=\dfrac{1}{2}AB=6\left(cm\right)\)
a: Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)
hay MN\(\perp\)AB
b: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=5(cm)
\(\Leftrightarrow MN=2.5\left(cm\right)\)

theo giả thiết ta có:BM=MA;BN=NC\(\Rightarrow\) MN là dg trung bình của tam giác ABC
\(\rightarrow\) MN song song vs BC\(\rightarrow\) góc BMN=BAC(đồng vị)
b/vì BM=MA ;BN=NC SUY RA:BM=MA=12:2=6 cm và BN=NC=BC:2=13:2=6.5 cm
áp dụng định lý pi-ta-go cho tam giác BNM vuông tại m:MN2=BN2+BM2
thay số:MN2=62+6.52
MN2=78.25 cm\(\Rightarrow\)MN=\(\sqrt{78.25}\)

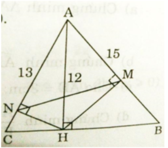
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
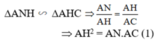
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
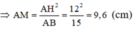
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()

a. xét tam giác AHB và tam giác ABC có:
góc H= góc A=90o
góc B chung
-> tam giác AHB~tam giác ABC (g.g)
b. thiếu đề rồi bạn.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
b: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
a) Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> MN//AC
Mà AC⊥AB(tam giác ABC vuông tại A)
=> MN⊥AB(từ vuông góc đến song song)
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(pytago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)
Ta có: MN là đường trung bình tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)