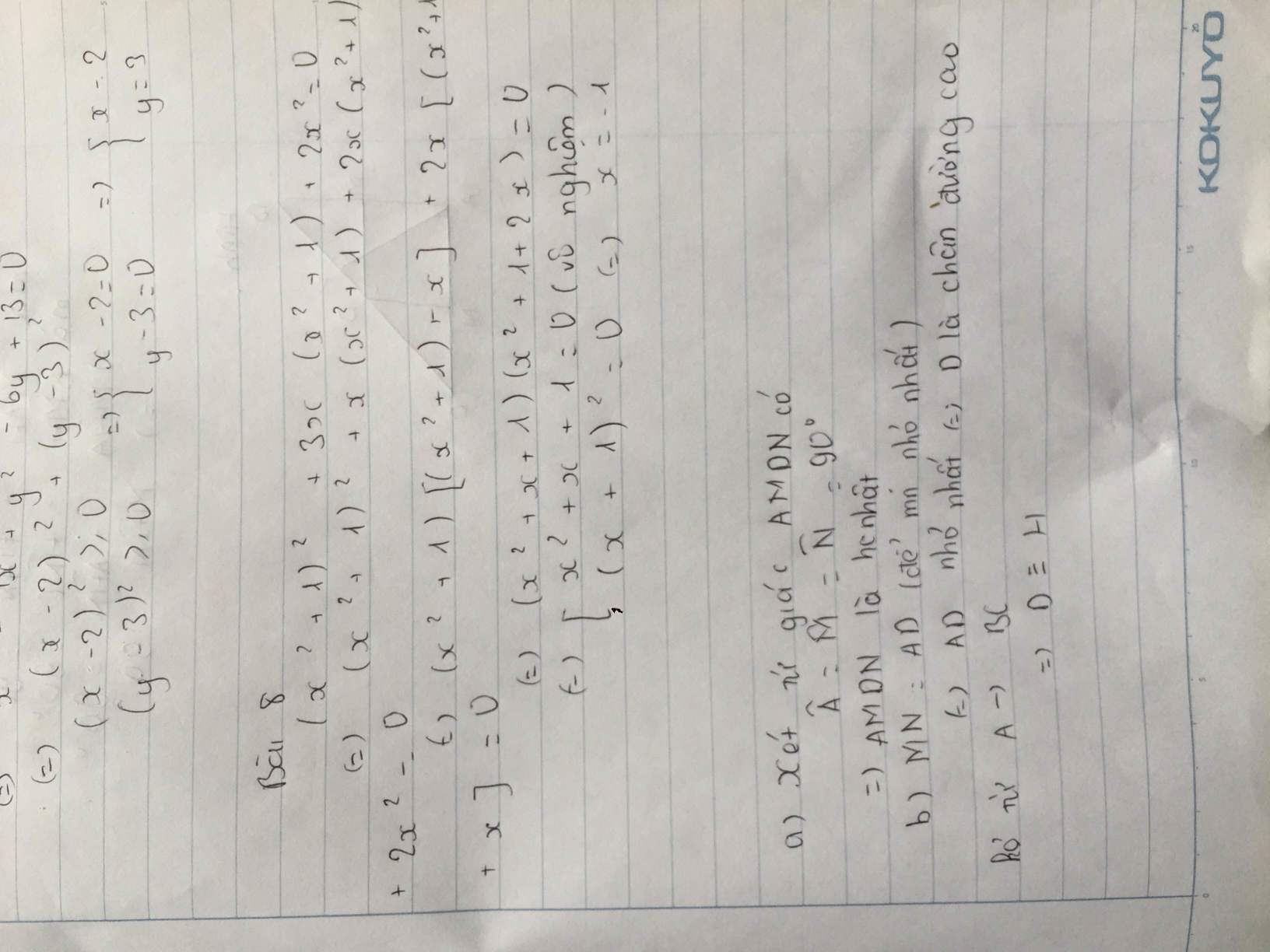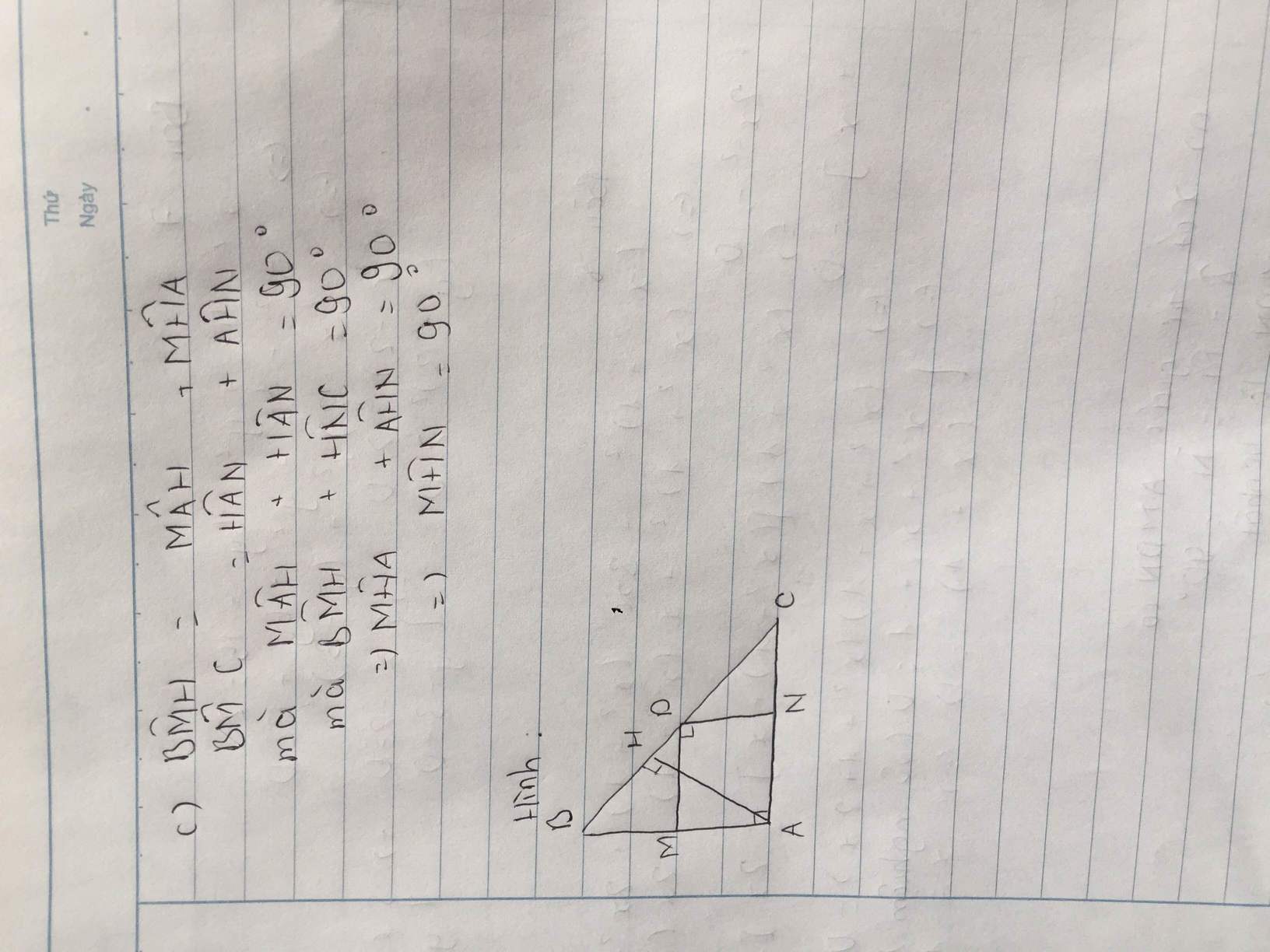Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
a. Vì DM⊥AB⇒ˆDMA=90oDM⊥AB⇒DMA^=90o,
DN⊥AC⇒ˆDNA=90oDN⊥AC⇒DNA^=90o,
ΔABC⊥A⇒ˆA=90oΔABC⊥A⇒A^=90o
⇒◊AMDN⇒◊AMDN là hình chữ nhật.
Áp dụng định lý Pitago vào ΔAMD⊥M,AM=3cm,AD=5cmΔAMD⊥M,AM=3cm,AD=5cm có:
MD=√AD2−AM2=4cmMD=AD2−AM2=4cm
⇒SAMDN=AM.DM=12cm2⇒SAMDN=AM.DM=12cm2
b. Gọi AD∩MN=E⇒EAD∩MN=E⇒E là trung điểm AD, MN
Mà AH⊥BCAH⊥BC
ΔAHD⊥H,EΔAHD⊥H,E là trung điểm cạnh huyền ADAD
⇒EH=EA=ED=EM=EN⇒EH=EA=ED=EM=EN
⇒ΔMHN⇒ΔMHN vuông tại HH
⇒ˆMHN=90o⇒MHN^=90o
c. Gọi G,IG,I là trung điểm AB,ACAB,AC suy ra GIGI là đường trung bình của ΔABCΔABC
⇒GI//BC⇒GI//BC
⇒GE,EI⇒GE,EI là đường trung bình ΔABD,ΔADC⇒GE//BD,EI//DCΔABD,ΔADC⇒GE//BD,EI//DC hay GE,EI//BCGE,EI//BC
⇒E∈GI⇒E∈GI
⇒⇒ Trung điểm EE của MNMN di chuyển trên đường trung bình ΔABCΔABC.

a,Xét tg ABC có: Góc A=90*,Góc M=90*,Góc N=90* <=>Tứ giác AMDN là hcn(vì có gócA=góc M=góc N=90*)

a: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
=>AMDN là hình chữ nhật
b: góc AHD=góc AMD=góc AND
=>A,H,D,M,N cùng nằm trên đường tròn đường kính AD
=>A,H,D,M,N cùng nằm trên đường tròn đường kính NM
=>góc NHM=90 độ

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
Suy ra: AD=MN
b: Xét tứ giác AMHD có góc AMD=góc AHD=90 độ
nên AMHD là tứ giác nội tiếp
=>A,M,H,D cùng thuộc 1 đường tròn (1)
Xét tứ giác AMDN có góc AMD+góc AND=180 độ
nên AMDN là tứ giác nội tiếp
=>A,M,D,N cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,M,H,D,N cùg thuộc 1 đường tròn
=>AMHN là tứ giác nội tiếp
=>góc AHM=90 độ

a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
Suy ra: AD=MN
b: Xét tứ giác AMHD có góc AMD=góc AHD=90 độ
nên AMHD là tứ giác nội tiếp
=>A,M,H,D cùng thuộc 1 đường tròn (1)
Xét tứ giác AMDN có góc AMD+góc AND=180 độ
nên AMDN là tứ giác nội tiếp
=>A,M,D,N cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,M,H,D,N cùg thuộc 1 đường tròn
=>AMHN là tứ giác nội tiếp
=>góc AHM=90 độ