Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=căn 10^2-6^2=8cm
BM là phân giác
=>AM/AB=CM/BC
=>AM/3=CM/5=(AM+CM)/(3+5)=1
=>AM=3cm; CM=5cm
b: Xét ΔMAB vuông tại A và ΔMDC vuông tại D có
góc AMB=góc DMC
=>ΔMAB đồng dạng với ΔMDC

1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
c: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

a: BD/AD=BC/AC=5/4
b: Xét ΔHBA và ΔABC có
góc BHA=góc BAC
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: Xét ΔDAC và ΔDKB có
góc DAC=góc DKB
góc ADC=góc KDB
=>ΔDAC đồng dạng với ΔDKB
=>DA/DK=DC/DB
=>DA*DB=DK*DC

a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
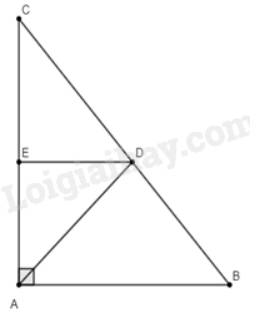
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
a/ Xét tg vuông BAC và tg vuông HAB có
\(\widehat{ACB}=\widehat{ABH}\) (cùng phụ với \(\widehat{BAC}\) )
b/
\(BC=\sqrt{AC^2-AB^2}\) (Pitago)
\(\Rightarrow BC=\sqrt{25^2-15^2}=20cm\)
\(\dfrac{MA}{AB}=\dfrac{MC}{BC}\) (T/c đường phân giác)
\(\Rightarrow\dfrac{MA}{15}=\dfrac{MC}{25}\Rightarrow\dfrac{MA}{MC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Rightarrow MC=\dfrac{AC}{3+5}x5=\dfrac{25}{8}x5=15,625cm\)
c/
\(AB^2=AH.AC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow AH=\dfrac{AB^2}{AC}\)
AM=AC-MC
HM=AM-AH
\(BH^2=AH.HC\)(trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
Xét tg vuông BHM
\(BM=\sqrt{BH^2+HM^2}\)
Ta có
\(AB\perp BC;MI\perp BC\) => MI//AB
\(\Rightarrow\dfrac{BI}{AM}=\dfrac{CI}{MC}\Rightarrow\dfrac{BI}{CI}=\dfrac{AM}{MC}\) (talet trong tg)
Từ đó tính được CI
Bạn tự thay số và tính toán
\(a.\) Xét \(\Delta BAC\) và \(\Delta HAB\) \(\left(\widehat{B}=\widehat{H}=90^o\right)\), ta có:
\(\widehat{A}\) là góc chung
\(\Rightarrow\Delta BAC\sim\Delta HAB\) \(\left(g-g\right)\)
\(b.\) Xét \(\Delta ABC\) vuông tại \(\widehat{B}\), ta có:
\(AC^2=AB^2+BC^2\) \(\left(Pytago\right)\)
\(\Rightarrow BC^2=AC^2-AB^2=25^2-15^2=625-225=400\)
\(\Rightarrow BC=\sqrt{400}=20\) \(\left(cm\right)\)
Do \(BM\) là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{BC}{MC}\) \(\Rightarrow\dfrac{AB}{AC-MC}=\dfrac{BC}{MC}\)
\(\Rightarrow AB\cdot MC=BC\cdot\left(AC-MC\right)\)
\(\Leftrightarrow AB\cdot MC=AC\cdot BC-BC\cdot MC\)
\(\Leftrightarrow AB\cdot MC+BC\cdot MC=AC\cdot BC\)
\(\Leftrightarrow MC\left(AB+BC\right)=AC\cdot BC\)
\(\Leftrightarrow MC=\dfrac{AC\cdot BC}{AB+BC}=\dfrac{25\cdot20}{15+20}=\dfrac{500}{35}=\dfrac{100}{7}\approx14,29\) \(\left(cm\right)\)